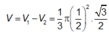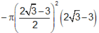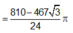Cho hình vuông ABCD cạnh a. Gọi N là điểm thuộc cạnh AD sao cho AN=2ND. Đường thẳng qua N vuông góc với BN cắt BC tại K. Tính thể tích V của khối tròn xoay tạo thành khi quay tứ giác ANKB quanh trục BK là

![]()
![]()
![]()

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
Công thức tính thể tích của khối trụ có bán kính đáy R và chiều cao h: V = π R 2 h
Công thức tính thể tích của khối nón có bán kính đáy R và chiều cao h: V = 1 3 π R 2 h
Cách giải:
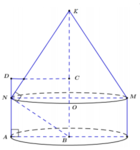
Khi quay tứ giác ANKB quanh trục BK ta được hình trụ có bán kính đáy AB, chiều cao AN và hình nón có bán kính đáy AB, chiều cao K O = B K − A N
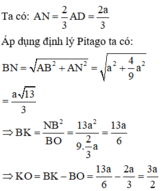
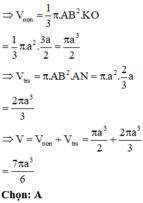

Đáp án D
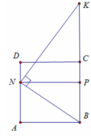
Gọi P là hình chiếu của N xuống BK
Khi quay tứ giác ANPB quanh trục BC ta được khối trụ có thể tích V 1 = πAB 2 . BP = 2 a 3 π 3
Lại có B P = 2 3 a ; N P = a suy ra P K = N P 2 B P = 3 a 2
Khi quay tam giác NKP quanh trục BC ta được khối nón có thể tích do đó V = V 1 + V 2 = 7 6 πa 3

Chọn C.
Phương pháp:
Dựng hình, xác định các hình tròn xoay tạo thành khi quay và tính tỉ số thể tích.
Cách giải:
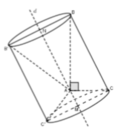
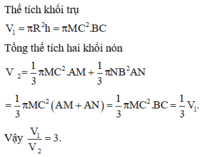

Đáp án A
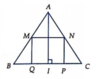
Gọi cạnh hình vuông là x. Ta có ![]()
![]()
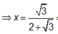
![]()
Gọi V 1 là thể tích hình nón khi quay tam giác ABC quanh trục trung tuyến AI , V 2 là thể tích hình trụ khi quay hình vuông MNPQ quanh trục AI thì