Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác đều. Tính góc giữa hai đường thẳng AB và CD.
A. 30 °
B. 60 °
C. 90 °
D. 120 °
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

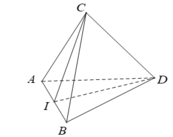
- Gọi I là trung điểm của AB. Vì ABC và ABD là các tam giác đều nên:
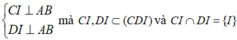
- Suy ra: AB ⊥ (CID) ⇒ AB ⊥ CD.
- Do đó, góc giữa AB và CD bằng 90 ° .

Chọn C.
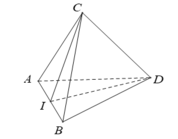
- Gọi I là trung điểm của AB. Vì ABC và ABD là các tam giác đều, nên: 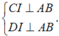
- Suy ra : 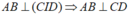
- Vậy góc giữa hai đường thẳng AB và CD bằng 90°

Gọi M là trung điểm AB
\(\Rightarrow\left\{{}\begin{matrix}CM\perp AB\\DM\perp AB\end{matrix}\right.\) (trong tam giác đều trung tuyến đồng thời là đường cao)
\(\Rightarrow AB\perp\left(CDM\right)\)
\(\Rightarrow AB\perp CD\)

Phương pháp
+) Dựng E sao cho ABCE là hình bình hành. Chứng minh d(AB;CD) = d(M;(CDE)).
+) Dựng khoảng cách từ M đến (CDE).
+) Áp dụng định lí Pytago trong các tam giác hình vuông tính CD.
Cách giải
Dựng E sao cho ABCE là hình bình hành như hình vẽ.


Gọi M là trung điểm của AB ta có:
Chọn C.