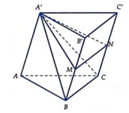
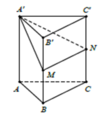
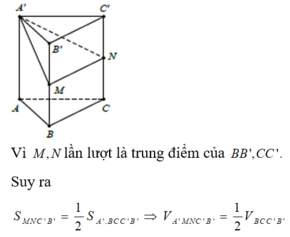
Cho khối lăng trụ tam giác A B C . A ' B ' C ' . Gọi M, N lần lượt là trung điểm của BB' và CC'. Mặt phẳng (A'MN) chia khối lăng trụ thành hai khối đa diện. Gọi V 1 là thể tích của khối đa thức diện chứa đỉnh B và V 2 là thể tích khôi đa diện còn lại. Tính tỉ số V 1 V 2
A. V 1 V 2 = 7 2
B. V 1 V 2 = 2
C. V 1 V 2 = 3
D. V 1 V 2 = 5 2

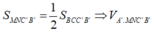
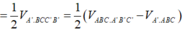

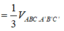
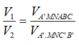
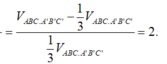
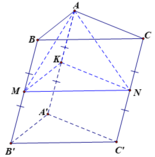
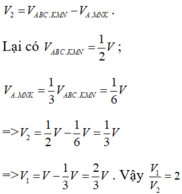
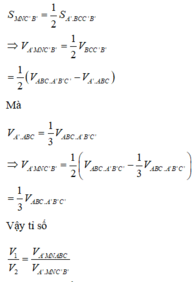
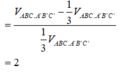
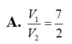
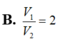
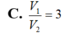
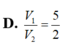


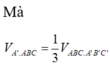
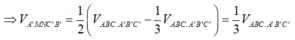
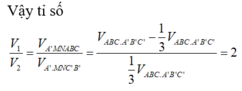
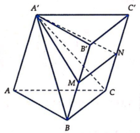
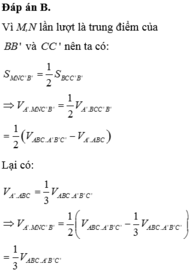
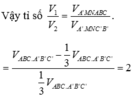


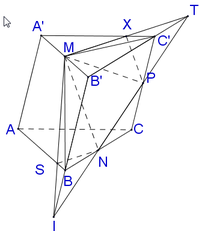
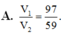
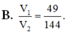
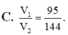
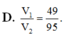

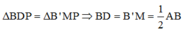
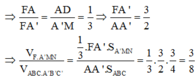
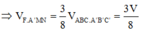

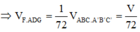

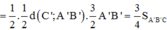
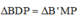
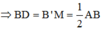
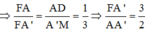
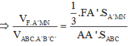
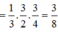
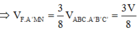
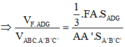
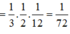
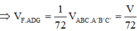
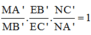
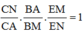
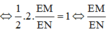
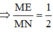
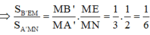
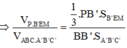
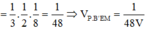
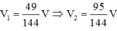
Chọn B