Cho hàm số f x = a x 2 + b x + c khi x ≥ 0 a x - b - 1 khi x < 0 . Khi hàm số f(x) có đạo hàm tại x 0 = 0 . Tính giá trị biểu thức T = a + 2b
A. -4
B. 0
C. -6
D. 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
14 tháng 1 2022
Bài 8:
a) f(-1) = (-1) - 2 = -3
f(0) = 0 - 2 = -2
b) f(x) = 3
\(\Rightarrow x-2=3\)
\(x=3+2\)
\(x=5\)
Vậy \(x=5\) thì f(x) = 3
c) Thay tọa độ điểm A(1; 0) vào hàm số, ta có:
VT = 0; VP = 1 - 2 = -1
\(\Rightarrow VT\ne VP\)
\(\Rightarrow\) Điểm A(1; 0) không thuộc đồ thị của hàm số đã cho
Thay tọa độ điểm B(-1; -3) vào hàm số, ta có:
VT = -3; VP = -1 - 2 = -3
\(\Rightarrow VT=VP=-3\)
\(\Rightarrow\) Điểm B(-1; -3) thuộc đồ thị hàm số đã cho
Thay tọa độ điểm C(3; -1) vào hàm số, ta có:
VT = -1; VP = 3 - 2 = 1
\(\Rightarrow VT\ne VP\)
\(\Rightarrow\) Điểm C(3; -1) không thuộc đồ thị hàm số đã cho.
CM
2 tháng 3 2019
a) Ta có:
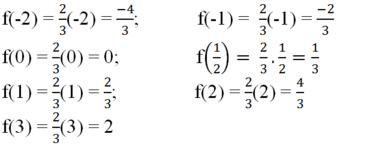
b) Ta có:
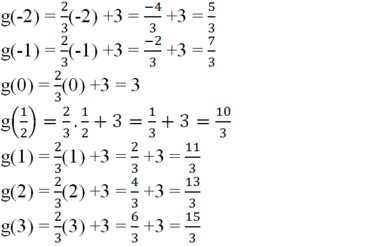
c) Từ kết quả câu a, b ta được bảng sau:
Nhận xét:
- Hai hàm số
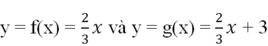
là hai hàm số đồng biến vì khi x tăng thì y cũng nhận được các giá trị tương ứng tăng lên.
- Cùng một giá trị của biến x, giá trị của hàm số y = g(x) luôn luôn lớn hơn giá trị tương ứng của hàm số y = f(x) là 3 đơn vị.
DT
0
LP
1
10 tháng 11 2019
\(f\left(x\right)=x^2-5x+6\)
a) +) \(f\left(-\frac{1}{3}\right)=\left(-\frac{1}{3}\right)^2-5.\left(-\frac{1}{3}\right)+6=\frac{70}{9}\)
+) \(f\left(\frac{1}{2}\right)=\left(\frac{1}{2}\right)^2-5.\frac{1}{2}+6=\frac{15}{4}\)
+) \(f\left(0\right)=0^2-5.0+6=6\)
+) \(f\left(1\right)=1^2-5.1+6=2\)
b) \(x^2-5x+6=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x-3=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=2\\x=3\end{cases}}\)
ok
25 tháng 10 2021
a: TXĐ: \(D=R\backslash\left\{-\dfrac{1}{2}\right\}\)
b: TXĐ: \(D=R\backslash\left\{-3;1\right\}\)
c: TXĐ: \(D=\left[-\dfrac{1}{2};3\right]\)
Đáp án C