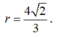Trong không gian với hệ tọa độ Oxyz cho hai mặt phẳng (P): x+2y+z+1=0 và (Q):2x-y+2z+4=0 . Gọi M là điểm thuộc mặt phẳng (P) sao cho điểm đối xứng của M qua mặt phẳng (Q) nằm trên trục hoành . Tung độ của điểm M bằng
A. 4.
B. 2.
C. -5
D. 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Gọi phương trình đường thẳng ∆ là
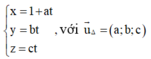
Vì ∆ nằm trong mặt phẳng (P)
![]()
Góc giữa hai đường thẳng ∆ và Oz là
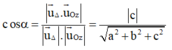
Ta có
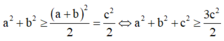
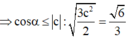
Khi cos α lớn nhất ⇒ α nhỏ nhất và bằng a r cos 6 3 . Xảy ra khi b = 2 c = 2 a
Do đó, phương trình đường thẳng ∆ là
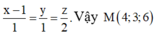

Chọn A
Điểm M(1;0;0) là 1 điểm thuộc (P)
Vì (P) // (Q) nên
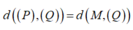
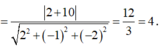
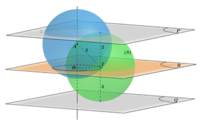
Giả sử I(a;b;c) là tâm của (S). Vì (S) tiếp xúc với cả (P) và (Q) nên bán kính mặt cầu (S) là:
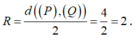
Do đó IA = 2 nên I luôn thuộc mặt cầu (T) tâm A, bán kính 2.
Ngoài ra
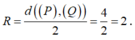
![]()
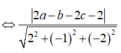
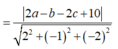
![]()
![]()
![]()
Do đó I luôn thuộc mặt phẳng (R): 2x-y-2z+4=0.
Gọi H là hình chiếu vuông góc của A lên (R). Vì A, (R) cố định nên H cố định.
Ta có
![]()
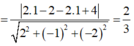
![]()
do đó tam giác AHI vuông tại H nên
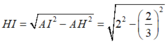
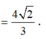
Vậy I luôn thuộc đường tròn tâm H, nằm trên mặt phẳng (R), bán kính