Cho hai vật dao động điều hòa cùng tần số góc ω , biên độ lần lượt là A 1 v à A 2 , A 1 + A 2 = 8 c m . Tại một thời điểm, vật một có li độ và vận tốc x 1 , v 1 ; vật hai có li độ và vận tốc x 2 , v 2 thỏa mãn x 1 v 2 + x 2 v 1 = 8 c m 2 / s . Tìm giá trị nhỏ nhất của ω
A. 2 rad/s
B. 0,5 rad/s.
C. 1 rad/s
D. 2,5 rad/s

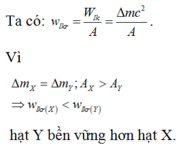
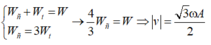
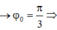
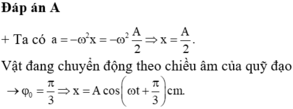
Chọn đáp án B
? Lời giải:
+ Với giải thiết bài toán x 1 v 1 + x 2 v 2 = 8 c m 2 / s ⇒ d x 1 x 2 d t = 8 c m 2 / s
Giả sử x 1 = A 1 cos ω t + φ 1 x 2 = A 2 cos ω t + φ 2
⇒ x 1 x 2 = A 1 A 2 cos ω t + φ 1 cos ω t + φ 2 = A 1 A 2 2 cos φ 1 − φ 2 + cos 2 ω t + φ 1 + φ 2
+ Thay vào phương trình đầu ta được ω = 8 − A 1 A 2 sin 2 ω t + φ 1 + φ 2
+ Với A 1 + A 2 2 ≥ A 1 A 2 ⇒ A 1 A 2 ≤ A 1 + A 2 2 2 = 16 c m 2
⇒ ω min khi mẫu số là lớn nhất vậy ω = 8 16 = 0 , 5 r a d / s