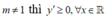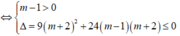Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(y=\dfrac{x^2-m^2+2m+1}{x-m}\) đúng không nhỉ?
\(y'=\dfrac{x^2-2mx+m^2-2m-1}{\left(x-m\right)^2}\)
Hàm đồng biến trên các khoảng xác định khi và chỉ khi:
\(x^2-2mx+m^2-2m-1\ge0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=m^2-\left(m^2-2m-1\right)\le0\)
\(\Leftrightarrow m\le-\dfrac{1}{2}\)
Hàm số xác định \(\Leftrightarrow\left(m-2\right)x^2-2\left(m-3\right)x+m-1\ge0\)
Đặt \(f\left(x\right)=\left(m-2\right)x^2-2\left(m-3\right)x+m-1\ge0\)
\(f\left(x\right)\ge0,\forall x\in R\Leftrightarrow\left\{{}\begin{matrix}a>0\\\Delta\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m-2>0\\\left[-2\left(m-3\right)\right]^2-4\left(m-2\right)\left(m-1\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>2\\4\left(m^2-6m+9\right)-4\left(m^2-3m+2\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow4m^2-24m+36-4m^2+12m-8\le0\)
\(\Leftrightarrow-12m+28\le0\)
\(\Leftrightarrow m\le\dfrac{7}{3}\)
\(KL:m\in(2;\dfrac{7}{3}]\)
\(y'=-x^2-2\left(m-2\right)x+m-2\)
Hàm nghịch biến trên TXĐ khi và chỉ khi \(y'\le0;\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-1< 0\left(đúng\right)\\\Delta'=\left(m-2\right)^2+m-2\le0\end{matrix}\right.\)
\(\Leftrightarrow\left(m-2\right)\left(m-1\right)\le0\)
\(\Leftrightarrow1\le m\le2\)
Chọn B.
Ta có: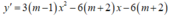
Nếu m = 1 thì y' = -18x-18 ⇔ x ≤ -1
Do đó m = 1 không thỏa mãn yêu cầu bài toán.
Nếu
