Đồ thị hàm số y = x 3 - x + 1 có bao nhiêu cặp điểm M, N đối xứng nhau qua điểm I(0;1)
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Gọi ![]()
![]()
là hai điểm trên (C) đối xứng nhau qua gốc tọa độ, ta có



Đáp án B

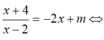
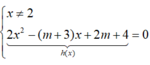
Điều kiện cần:
Để ∆ cắt (C) tại hai điểm phân biệt thì phương trình h(x) = 0 có hai nghiệm phân biệt khác 2, tức là
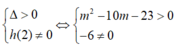
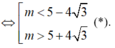
Điều kiện đủ:
Gọi I là trung điểm của AB, ta có:
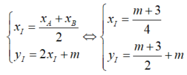
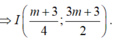

![]()
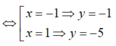
Vậy tọa hai điểm cần tìm là
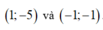

TH1 : Đồ thị hàm số y = 3mx2 - (m - 9)x + 8 - m2 có hai điểm phân biệt đối xứng nhau qua gốc tọa độ khi hàm số trên là hàm số lẻ trên tập xác định R
Khi đó f(x) + f(-x) = 0
⇒ 3mx2 + 3mx2 - (m - 9)x + 8- m2 + (m - 9)x - m2 + 8 = 0
⇒ 6mx2 + 16 = 0 (không có m)

Đáp án A
Phương pháp: Tham số hóa điểm thuộc đồ thị hàm số (C).
Lấy điểm đối xứng với điểm đó qua O (Điểm (a;) đối xứng với điểm (-a;-b)qua gốc tọa độ O).
Cho điểm đối xứng vừa xác định thuộc (C).
Cách giải:
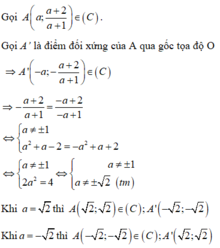
Chú ý và sai lầm : Có thể thử trực tiếp từng đáp án và suy ra kết quả.

Đáp án là A.
Ta có: y , = 3 x 2 - 6 m x = 0 ⇔ x = 0 x = 2 m
Để đồ thị hàm số có 2 cực trị thì m ≢ 0 suy ra A(0; 4 m 8 ),B(2m;0)
YCBT, ta có m = ± 1 2

Chọn D
Xét y = log a x ; ( 0 < a ≠ 1 ) ( C 0 ), y = f(x)(C), (C) đối xứng với ( C 0 ) qua I(2;1).
Gọi điểm ![]() đối xứng với nhau qua điểm I(2;1), ta có:
đối xứng với nhau qua điểm I(2;1), ta có:
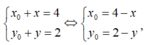
thay vào phương trình của ( C 0 ) ta được:
![]()
![]()
Suy ra ![]() = -2017
= -2017
Như vậy, ![]()
Chọn A