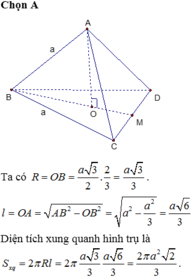
Cho tứ diện ABCD cạnh a. Diện tích xung quanh hình trụ có đáy là đường tròn ngoại tiếp tam giác BCD và có chiều cao bằng chiếu cao tứ diện ABCD là:
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
Gọi r là bán kính đường tròn đáy và h là chiều cao tứ diện, ta có Sxq = 2 π .r.h.
Nếu gọi M là trung điểm CD và G là trọng tâm tam giác BCD thì ta có
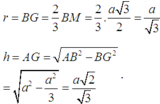
Vậy
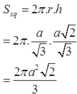

Đáp án D
Gọi r là bán kính đường tròn đáy và h là chiều cao tứ diện, ta có S x q = 2 π . r . h
Nếu gọi M là trung điểm CD và G là trọng tâm tam giác BCD thì ta có
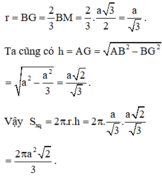

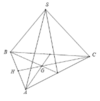
r = G H = 1 3 C H = 1 3 . 4 . 3 2 = 2 3 3
h = A G = A C 2 - C G 2 = 4 2 - 4 . 3 2 . 2 3 2 = 4 6 3
S x q = 2 πrl = 2 π . 2 3 3 . 4 6 3 = 16 2 3 π
Đáp án cần chọn là A

Đáp án A
Ta có r t r = G H = 1 3 C H = 2 3 3
h t r u = A G = A C 2 - C G 2 = 4 6 3
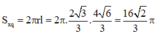

Đáp án A.
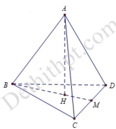
Dựng hình như hình vẽ bên ta có:
Bán kính đường tròn nội tiếp đáy:
r = H M = 1 3 B M = 4 3 6
Chiều cao:
h = A H = A B 2 − B H 2 = 4 2 − 4 3 3 2 = 4 6 3
Do đó S x q T = 2 π h = 16 π 2 3 .