Cho số phức z = 2 + 4i. Tính hiệu phần thực và phần ảo của z.
A. 2.
B. 2 5 .
C. -2.
D. 6.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
15 tháng 8 2018
Chọn đáp án C
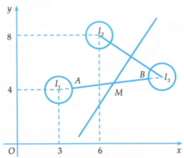
Gọi M 1 , M 2 , M lần lượt là điểm biểu diễn của các số phức z 1 , 2 z 2 , z trên mặt phẳng tọa độ Oxy.
Do z 1 - 3 - 4 i = 1 nên quỹ tích điểm M 1 là đường tròn C 1 có tâm I 1 3 ; 4 và bán kính R = 1
Do z 2 - 3 - 4 i = 1 2 ⇔ 2 z 2 - 6 - 8 i = 1 nên quỹ tích điểm M 2 là đường tròn C 2 có tâm I 2 6 ; 8 và bán kính R = 2
Ta có điểm M(a; b) thỏa mãn 3a - 2b = 12 nên quỹ tích điểm M là đường thẳng d: 3x - 2y - 12 = 0
Khi đó
Gọi C 3 là đường tròn đối xứng với đường tròn C 2 qua đường thẳng d.
Ta tìm được tâm của C 3 là I 3 138 13 ; 64 13 và bán kính R = 1
Khi đó
với M 3 ∈ C 3 và A, B lần lượt là giao điểm của đường thẳng I 1 I 3 với hai đường tròn C 1 , C 3 (quan sát hình vẽ).
Dấu "=" xảy ra khi và chỉ khi M 1 ≡ A và M 3 ≡ B
Vậy P m i n = A B + 2 = I 1 I 3 = 3 1105 13
CM
27 tháng 9 2017
a) Tập hợp các điểm thuộc đường thẳng x = -2
b) Tập hợp các điểm thuộc đường thẳng y = 3
c) Tập hợp các điểm thuộc mặt phẳng nằm giữa hai đường thẳng song song x = -1 và x = 2 (hình có gạch sọc)
d) Phần mặt phẳng giới hạn bởi các đường thẳng song song y = 1 và y = 3( kể cả các điểm thuộc hai đường thẳng đó).
e) Các điểm thuộc hình chữ nhật với các cạnh nằm trên các đường thằng x = -2, x = 2 , y = -2, y = 2.
Đáp án C