Cho hàm số y=f(x). Hàm số y=f’(x) có đồ thị như hình vẽ dưới đây.
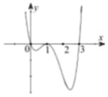
Tìm m để hàm số y = f ( x 2 + m ) có ba điểm cực trị
A. mÎ(3;+∞)
B. mÎ[0;3]
C. mÎ[0;3)
D. mÎ(-∞;0)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn A.
Theo đồ thị ta có: f'(x) > 0 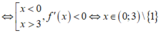
Ta có: ![]()
Cho y' = 0
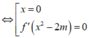
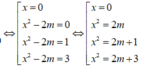
Để hàm số có 3 điểm cực trị thì phương trình y' = 0 phải có 3 nghiệm bội lẻ
Ta thấy x = 0 là một nghiệm bội lẻ
Dựa vào đồ thị của y = f'(x) ta thấy x = 1 là nghiệm bội lẻ (không đổi dấu), do đó ta không xét trường hợp ![]()
Suy ra để hàm số có 3 điểm cực trị thì
TH1: x 2 = 2m có 2 nghiệm phân biệt khác 0 và x 2 = 2m + 3 vô nghiệm hoặc có nghiệm kép bằng 0
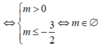
TH2. x 2 = 2m + 3 có 2 nghiệm phân biệt khác 0 và x 2 = 2m vô nghiệm hoặc có nghiệm kép bằng 0
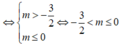
Vậy hàm số của 3 điểm cực trị khi