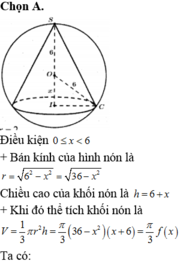
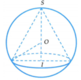
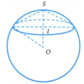
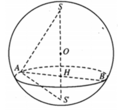
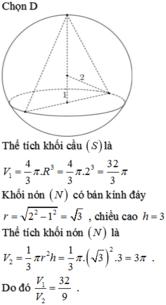
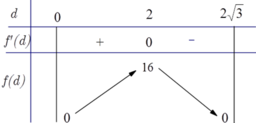
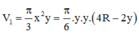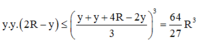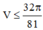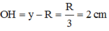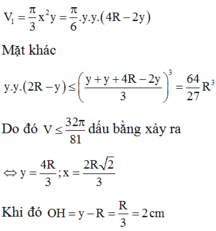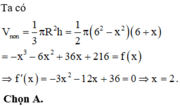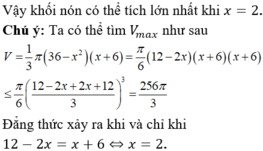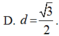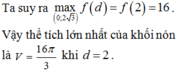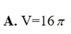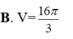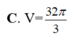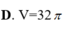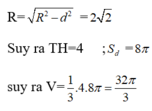Cho khối tâm cầu O bán kính bằng 6cm. Mặt phẳng (P) cách O một khoảng là x, cắt khối cầu theo một hình tròn (C). Một khội nón có đỉnh thuộc mặt cầu, đáy là hình tròn (C). Biết khối nón có thể tích lớn nhất, giá trị của x bằng
A. 2cm
B. 3cm
C. 4cm
D. 0cm