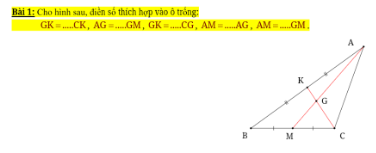
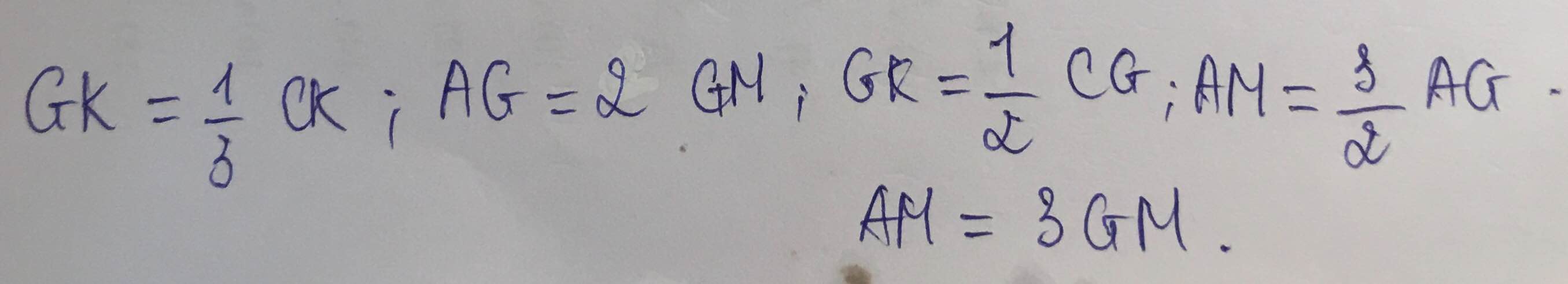Giúp mình với , GẤP LẮM...
Đọc tiếp
Giúp mình với , GẤP LẮM !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LJ
3
DT
Đỗ Thanh Hải
CTVVIP
24 tháng 4 2021
II
1 B
2 C
3 A
4 D
5 C
6 B
III
1 Where do they live?
2 Why do you like "Tom and Jerry"
3 When do they do their homework?
4 What is that?
5 What vegetable do you like?
25 tháng 12 2021
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
DT
2
10 tháng 5 2021
Giải:
a)\(\dfrac{3}{4}x-\dfrac{1}{3}=\dfrac{-5}{6}\)
\(\dfrac{3}{4}x=\dfrac{-5}{6}+\dfrac{1}{3}\)
\(\dfrac{3}{4}x=\dfrac{-1}{2}\)
\(x=\dfrac{-1}{2}:\dfrac{3}{4}\)
\(x=\dfrac{-2}{3}\)
b)\(\left(2\dfrac{4}{5}x-0,2\right):\dfrac{4}{5}=\dfrac{7}{8}\)
\(\dfrac{14}{5}x-\dfrac{1}{5}=\dfrac{7}{8}.\dfrac{4}{5}\)
\(\dfrac{14}{5}x-\dfrac{1}{5}=\dfrac{7}{10}\)
\(\dfrac{14}{5}x=\dfrac{7}{10}+\dfrac{1}{5}\)
\(\dfrac{14}{5}x=\dfrac{9}{10}\)
\(x=\dfrac{9}{10}:\dfrac{14}{5}\)
\(x=\dfrac{9}{28}\)
c) \(\dfrac{1}{4}+\dfrac{1}{3}:\left|2x-1\right|=\dfrac{11}{12}\)
\(\dfrac{1}{3}:\left|2x-1\right|=\dfrac{11}{12}-\dfrac{1}{4}\)
\(\dfrac{1}{3}:\left|2x-1\right|=\dfrac{2}{3}\)
\(\left|2x-1\right|=\dfrac{1}{3}:\dfrac{2}{3}\)
\(\left|2x-1\right|=\dfrac{1}{2}\)
⇒2x-1=\(\dfrac{1}{2}\) hoặc 2x-1=\(\dfrac{-1}{2}\)
x=\(\dfrac{3}{4}\) hoặc x=\(\dfrac{1}{4}\)
10 tháng 5 2021
câu a nha \(\dfrac{3}{4}x-\dfrac{1}{3}=-\dfrac{5}{6}\)
\(\dfrac{3}{4}x=-\dfrac{5}{6}+\dfrac{1}{3}\)
\(\dfrac{3}{4}x=-\dfrac{3}{6}\)
\(x=-\dfrac{3}{6}:\dfrac{3}{4}\)
\(x=-\dfrac{6}{4}.\dfrac{4}{3}\)
\(x=-\dfrac{24}{12}=-2\)
HV
30 tháng 11 2021
1 do you do
2 had done - went
3 went - had read
4 will attend
5 hadn't worn
6 to be
7 weren't sleeping - were playing
8 to be
9 had lived - moved
10 locking
11 had work - retired
12 told - had learned
13 won't call
14 had met
30 tháng 11 2021
do you do
had done-went
went- had read
will attend
hadn't worn
to be
LG
0
T
0
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2022
Coi như bài toán đã cho là x;y;z hết từ điều kiện đến biểu thức (lẫn lộn abc với xyz)
Đặt \(\left(x^3;y^3;z^3\right)=\left(a^2;b^2;c^2\right)\Rightarrow abc=1\)
Ta có: \(Q=\dfrac{1}{a^2+b^2+b^2+1+2}+\dfrac{1}{b^2+c^2+c^2+1+2}+\dfrac{1}{c^2+a^2+a^2+1+2}\)
\(Q\le\dfrac{1}{2ab+2b+2}+\dfrac{1}{2bc+2c+2}+\dfrac{1}{2ca+2a+2}\)
\(Q\le\dfrac{1}{2}\left(\dfrac{1}{ab+b+1}+\dfrac{ab}{ab.bc+abc+ab}+\dfrac{b}{cab+ab+b}\right)\)
\(Q\le\dfrac{1}{2}\left(\dfrac{1}{ab+b+1}+\dfrac{ab}{b+1+ab}+\dfrac{b}{1+ab+b}\right)=\dfrac{1}{2}\)
