Cho hàm số y=f(x) có bảng biến thiên như sau:
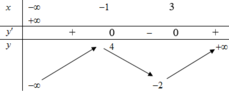
Số nghiệm của phương trình 2 f ( x ) + 1 = 0 là:
A. 0
B. 3
C. 1
D. 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
14 tháng 6 2018
Đúng(0)
Những câu hỏi liên quan
CM
1 tháng 10 2018
Đáp án A
Phương pháp:
+) Số nghiệm của phương trình f(x) = m là số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m.
+) Dựa vào BBT để xác định số giao điểm của các đồ thị hàm số.
Cách giải:
Ta có: 
Số nghiệm của phương trình (*) là số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = - 3 2
Dựa vào BBT ta thấy đường thẳng y = - 3 2 cắt đồ thị hàm số y = f(x) tại 4 điểm phân biệt
=>Phương trình có 4 nghiệm phân biệt
CM
2 tháng 12 2018
Đáp án B
f ( x ) − 2 = 0 ⇔ f ( x ) = 2
Dựa vào bảng biến thiên để xét sự tương giao giữa đồ thị hàm số f(x) và đường thẳng x = 2 ta thấy pt có 3 nghiệm
CM
7 tháng 2 2018
Đáp án B.
f ( x ) - 2 = 0 ⇔ f ( x ) = 2
Dựa vào bảng biến thiên để xét sự tương giao giữa đồ thị hàm số f(x) và đường thẳng x=2 ta thấy pt có 3 nghiệm.
CM
27 tháng 11 2017
Đáp án là B
Ta có Phương trình đã cho là phương trình hoành độ giao điểm của đồ thị hàm số với đường thẳng y = −2 . Dựa vào bảng biến thiên ta thấy phương tình có 2 nghiệm.
