Cho tam giác ABC có ba góc nhọn. Vẽ các đường cao AI, BK, CL của tam giác ấy. Gọi H là giao điểm của các đường cao vừa vẽ. Chứng minh KB là tia phân giác của ∠ LKI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 10 2018
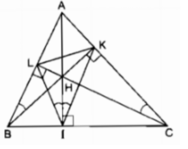
Vì ∆ ABC là tam giác nhọn nên ba đường cao cắt nhau tại điểm H nằm trong tam giác ABC.
Tứ giác BIHL nội tiếp.
Tứ giác CIHK nội tiếp.
Từ (1), (2) suy ra:
CM
25 tháng 9 2018
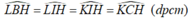
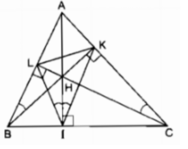
Vì ∆ ABC là tam giác nhọn nên ba đường cao cắt nhau tại điểm H nằm trong tam giác ABC.
Tứ giác AKHL có 
Tứ giác AKHL nội tiếp.
Tứ giác BIHL có 
Tứ giác BIHL nội tiếp.
Tứ giác CIHK có 
Tứ giác CIHK nội tiếp.
Tứ giác ABIK có 
K và I nhìn đoạn AB dưới một góc vuông nên tứ giác ABIK nội tiếp. Tứ giác BCKL có 
K và L nhìn đoạn BC dưới một góc vuông nên tứ giác BCKL nội tiếp.
Tứ giác ACIL có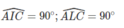 
I và L nhìn đoạn AC dưới một góc vuông nên tứ giác ACIL nội tiếp.
22 tháng 11 2022
a: Xét tứ giác BFEC có góc BFC=góc BEC=90 độ
nên BFEC là tứ giác nội tiếp
b: Xét (O) có
ΔBCK nội tiếp
BK là đường kính
Do đó: ΔBCK vuông tại C
=>CK//AH
Xét (O) có
ΔBAK nội tiếp
BK là đường kính
Do đó: ΔBAK vuông tại A
=>AK//CH
Xét tứ giác CHAK có
CH//AK
CK//AH
DO đó: CHAK là hình bình hành
13 tháng 6 2023
a: góc AEB=góc ADB=90 độ
=>AEDB nội tiếp
b,c: M ở đâu vậy bạn?
Vì ∆ ABC là tam giác nhọn nên ba đường cao cắt nhau tại điểm H nằm trong tam giác ABC.