Cho hình chóp tứ giác đều S.ABCD có SA = a và
S
A
B
⏜
=
11
π
24
.
Gọi Q là trung điểm của cạnh SA. Trên các cạnh SB, SC, SD lần lượt lấy các điểm M, N, P không trùng với các đỉnh của hình chóp. Tìm giá trị nhỏ nhất của tổng
A
M
+
M
N
+
N
P
+
P
Q
theo a A.
a
2
sin
...
Đọc tiếp
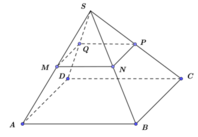
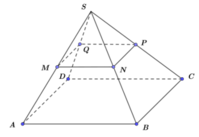
Cho hình chóp tứ giác đều S.ABCD có SA = a và S A B ⏜ = 11 π 24 . Gọi Q là trung điểm của cạnh SA. Trên các cạnh SB, SC, SD lần lượt lấy các điểm M, N, P không trùng với các đỉnh của hình chóp. Tìm giá trị nhỏ nhất của tổng A M + M N + N P + P Q theo a
A. a 2 sin 11 π 24 3
B. a 3 2
C. a 2 4
D. a 3 sin 11 π 12 3
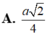
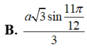
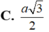
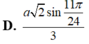
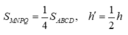
Chọn đáp án B
Do S.ABCD là hình chóp tứ giác đều nên mỗi mặt bên là một tam giác cân tại đỉnh S.
Theo giả thiết ta có
Cắt hình chóp theo cạnh bên SA rồi trải các mặt bên thành một mặt phẳng ta được hình vẽ bên sao cho khí ghép lại thì A ≡ A '
Suy ra A S A ' ⏜ = 4 . A S B ⏜ = π 3 và ∆ S A A ' đều cạnh SA = a
Khi đó tổng AM + MN + NP + PQ là tổng của các đường gấp khúc.
Tổng này đạt nhỏ nhất bằng AQ nếu xảy ra trường hợp các điểm A, M, N, P, Q thẳng hàng.
Mà ∆ S A A ' đều có Q là trung điểm SA nên A Q = S A 3 2 = a 3 2
Vậy m i n A M + M N + N P + P Q = a 3 2