Cho đường tròn (O) và điểm A cố định trên đường tròn. Gọi xy là tiếp tuyến với đường tròn tại A. Từ một điểm M nằm trên xy, vẽ tiếp tuyến MB với đường tròn. Gọi H là trực tâm của tam giác MAB. Tứ giác AOBH là hình gì?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 11 2019
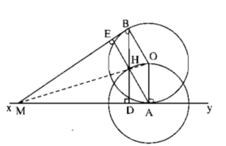
H cách A cố định một khoảng bằng OA không đổi nên H di chuyển trên đường tròn (A; AO).
CM
25 tháng 12 2018
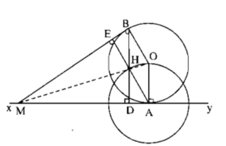
Gọi BD, AE là đường cao của ∆ MAB. Ta có ΔMAE = ∆ MBD (cạnh huyền – góc nhọn) nên ME = MD, ∆ MHE = ∆ MHD (cạnh huyền – cạnh góc vuông) nên ∠ (EMH) = ∠ (DMH). MH và MO đều là tia phân giác của góc AMB nên M, H, O thẳng hàng.
9 tháng 2 2021
H cách A cố định một khoảng bằng OA không đổi nên H di chuyển trên đường tròn (A ; AO).
Chúc bạn học tốt
30 tháng 9 2021
a: Xét (O) có
MA là tiếp tuyến có A là tiếp điểm
MB là tiếp tuyến có B là tiếp điểm
Do đó: MA=MB
Xét ΔMAB có MA=MB
nên ΔMAB cân tại M
Suy ra: \(\widehat{MAB}=\widehat{MBA}\)
Xét ΔDAB vuông tại D và ΔEBA vuông tại E có
BA chung
\(\widehat{DBA}=\widehat{EAB}\)
Do đó: ΔDAB=ΔEBA
Suy ra: \(\widehat{DAB}=\widehat{EBA}\)
hay \(\widehat{HAB}=\widehat{HBA}\)
Xét ΔHBA có \(\widehat{HAB}=\widehat{HBA}\)
nên ΔHBA cân tại H
Suy ra: HA=HB
hay H nằm trên đường trung trực của AB(1)
Ta có:MA=MB
nên M nằm trên đường trung trực của AB(2)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(3)
Từ (1), (2) và (3) suy ra O,H,M thẳng hàng
Tứ giác AOBH có BH // OA, AH // OB và OA = OB nên là hình thoi.