Tính diện tích lớn nhất của hình chữ nhật ABCD nội tiếp trong nửa đường tròn có bán kính 10cm (hình vẽ)
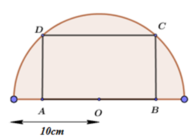
A. 160
B. 100
C. 80
D. 200
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
31 tháng 3 2017
Đúng(0)
Những câu hỏi liên quan
CM
19 tháng 6 2017
Đáp án B
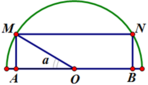
Dựng hình như hình vẽ. Đặt M N = 2 x ⇒ N P = R 2 − x 2
Khi đó S = 2 x . R 2 − x 2 ≤ R 2 − x 2 + x 2 = R 2
Vậy S max = 36 c m 2
13 tháng 5 2023
Đặt AB=x; BC=y
=>x+y=28 và x^2+y^2=20^2=400
=>x=16; y=12
=>S=16*12=192cm2
CM
29 tháng 9 2019
Đáp án C
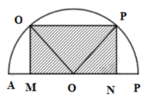
Giả sử khoảng đất được mô phỏng như hình vẽ. Mảnh vườn trồng hoa là AMNB
Khi đó R=OM=1m.
Gọi a = M O A ^ . Ta có MA=OM.sin a(m) và AB=2AO=2OM.cos a=2cos a(m).
Diện tích mảnh đất trồng hoa là S A M N B = M A . A B = 2 sin a cos a = sin 2 a ≤ 1 .
Vậy diện tích mảnh đất trồng hoa lớn nhất bằng 1( m 2 ) khi 2 a = 90 ° ⇔ a = 45 °
BO
19 tháng 1 2017
Chu vi hình chữ nhật :
(10 + 6) x 2 = 32 m
DT hình chữ nhật :
10 x 6 = 60 m2
Diện tích 2 nửa đường tròn bán kính AB và DC :
10 x 10 x 3,14 = 314 m2
Diện tích 2 nửa đường tròn bán kính BC và AD :
6 x 6 x 3,14 = 113,04 m2
DT cả hình đó :
60 + 314 + 113,04 = 487,04m2
DT tam giác ABD :
60 : 2 = 30 m2
13 tháng 5 2023
Đặt AB=x, BC=y
Theo đề, ta có:
x+y=14 và x^2+y^2=100
=>x=8; y=6
=>S=8*6=48cm2
