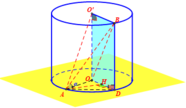
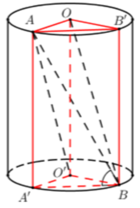
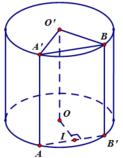
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn tâm O’ lấy điểm B. Đặt α là góc giữa AB và đáy. Biết rằng thể tích khối tứ diện OO’AB đạt giá trị lớn nhất. Khẳng định nào sau đây là đúng ? Tính bán kính mặt cầu ngoại tiếp hình chóp theo a.
A. tan α = 2
B. tan α = 1 2
C. tan α = 1 2
D. tan α = 1


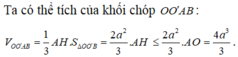
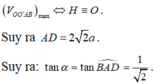

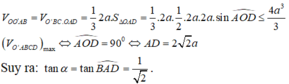
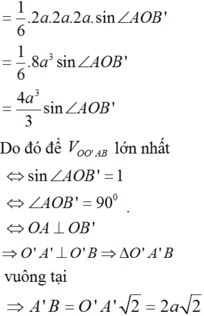
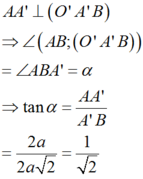
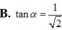



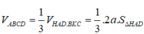




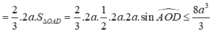
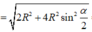
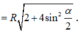
Đáp án B
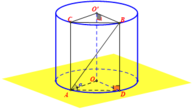
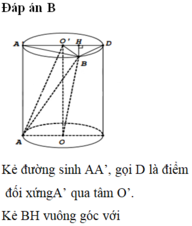
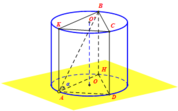
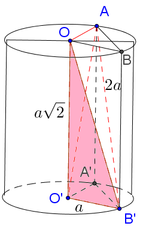
Kẻ đường sinh AA’, gọi D là điểm đối xứng A’ qua tâm O’.
Kẻ BH vuông góc với A ' D ⇒ B H ⊥ A O O ' A ' ⇒ V O O ' A B = 1 3 . B H . S Δ O O ' A
Mà S Δ O O ' A = 1 2 . O O ' . O A = 2 a 2 ⇒ V O O ' A B = 2 a 2 3 x B H
Để V O O ' A B lớn nhất ⇔ B H = B O ' H ≡ O ' ⇒ A ' B = 2 a 2
Tam giác AA’B vuông tại A’, có tan A B A ' ^ = A A ' A ' B = 2 a 2 a 2 = 1 2
Vậy A B ; O ' ^ = A B ; A ' B ^ = A B A ' ^ = α ⇒ tan α = 1 2