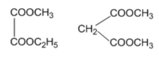
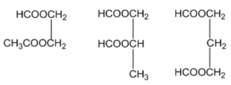
Đốt cháy hoàn toàn a mol một este no, đơn chức mạch hở X, cần b mol O2, tạo ra c mol hỗn hợp CO2 và H2O. Biết c = 2(b-a). Số đồng phân este của X là
A. 4
B. 3
C. 2
D. 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn đáp án A
Giả sử X là CnH2nO2
C n H 2 nO 2 + 3 n - 2 2 O 2 → nCO 2 + nH 2 O
Giả sử có 1 mol X → 2 n = 2 ( 3 n - 2 2 - 1 ) → n = 4.
Vậy X là C4H8O2.
Có 4 đồng phân este của X là
1. HCOOCH2CH2CH3
2. HCOOCH(CH3)2
3. CH3COOCH2CH3
4. CH3CH2COOCH3

Đáp ánC
Vì X là este no, đơn chức mạch hở nên ![]() và X có 2 nguyên tử O trong phân tử.
và X có 2 nguyên tử O trong phân tử.
Áp dụng định luật bảo toàn nguyên tố oxi có:
![]() hay 2a + 2b = l,5c
hay 2a + 2b = l,5c
⇔a + b = 0,75c
mà theo giả thiết có b - a = 0,5c nên
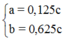
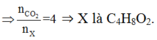
Các đồng phân este của X: HCOOCH2CH2CH3, HCOOCH(CH3)2, CH3COOC2H5, C2H5COOCH3.

Chọn đáp án D
Nhận thấy a = b-d → chứng tỏ trong X chứa 2 liên kết π = 1 π COO + 1π C=C
+ X có dạng CnH2n-2O2
+ Bảo toàn nguyên tố O ⇒ 2a + 2. V 22 , 4 = 2b + d → 2a + 2. 100 , 8 a 22 , 4 = 2b + d → 11a = 2b+ d
+ Cộng 2 vế 12a = 3b ⇒ số C trong X là b : a = 4a : a = 4 ⇒ X có công thức C4H6O2
Số đồng phân thoả mãn điều kiện của X gồm:
(1) HCOOC=CH-CH3.
(2) HCOOC-CH=CH2.
(3) HCOOC(CH3)=CH2.
(4) CH3COOCH=CH2.
(5) CH2=CH-COOCH3.

Chọn đáp án D
♦ giải đốt 5 , 52 g a m ( E + T ) + 0 , 27 m o l O 2 → t 0 C O 2 + 0 , 20 m o l H 2 O
BTKL có m C O 2 = 10 , 56 g a m → n C O 2 = 0 , 24 m o l
giả thiết → este E dạng CnH2nO2 và este T dạng CmH2m – 2O2 (n ≥ 2; m ≥ 3).
→ tương quan: ∑ n C O 2 – n H 2 O = n T = 0 , 24 – 0 , 2 = 0 , 04 m o l
Lại có n E + T = 1 2 n O t r o n g E + T = 0 , 07 m o l (bảo toàn O phương trình đốt cháy)
Suy ra n E = 0 , 03 m o l
→ ∑ n C O 2 = 0 , 03 n + 0 , 04 m = 0 , 24
→ 3n + 4m = 24.
Nghiệm nguyên duy nhất n = 4; m = 3
→ CTPT của este E là C4H8O2.
→ các đồng phân cấu tạo của E thỏa mãn là: HCOOCH2CH2CH3 (1);
HCOOCH(CH3)2 (2);
CH3COOCH2CH3 (3);
C2H5COOCH3 (4).
Tổng có 4 đồng phân cấu tạo

Chọn đáp án C

Bảo toàn nguyên tố O:
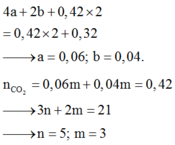
Este E là C 5 H 8 O 4 ; este T là C 3 H 4 O 2 ( H C O O C H = C H 2 )