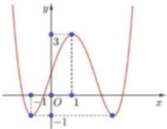
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào sau đây?
A. - ∞ ; - 1
B. (-1;3)
C. 1 ; + ∞
D. - ∞ ; + ∞
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn D.
Phương pháp
Sử dụng cách đọc đồ thị hàm số để tìm khoảng đồng biến, nghịch biến
Xét từ trái qua phải trên khoảng (a;b) nếu đồ thị đi xuống thì hàm số nghịch biến trên (a;b), nếu đồ thị đi lên thì hàm số đồng biến trên (a;b).
Cách giải:
Từ hình vẽ ta thấy : Xét từ trái qua phải thì đồ thị hàm số đi lên trên khoảng (-1;1).
Nên hàm số đồng biến trên (-1;1) suy ra hàm số đồng biến trên (0;1).

Đáp án là D
Quan sát đồ thị hàm số ta thấy trong khoảng (-1;0) thì đồ thị hàm số đi lên hàm số đồng biến trong khoảng (-1;0)

Chọn đáp án B.
Phương pháp
Dựa vào đồ thị hàm số, xác định khoảng mà trong khoảng đó theo chiều từ trái sang phải đồ thị hàm số luôn đi lên.
Cách giải
Dựa vào đồ thị hàm số ta thấy hàm số y=f(x) đồng biến trên khoảng (0;+∞)

Đáp án D
Phương pháp:
Sử dụng kĩ thuật đọc đồ thị hàm số. Các khoảng đồ thị hàm số đi lên là các khoảng đồng biến của hàm số.
Cách giải:
Quan sát đồ thị hàm số ta thấy trong khoảng (-1;0) thì đồ thị hàm số đi lên hàm số đồng biến trong khoảng (-1;0)

Đáp án B
Từ đồ thị hàm số ta thấy:
+ Hàm số đồng biến trên khoảng (-3;-1)

Đáp án C
Dựa vào đồ thị hàm số, ta thấy đồ thị hàm số đi lên trên khoảng (1;3)
Suy ra hàm số đồng biến trên (2;3)

HD: Hàm số đã cho đồng biến trên (1;3) nên cũng đồng biến trên (2;3). Chọn C.