Xét tứ diện ABCD có các cạnh A B = B C = C D = D A = 1 và AC, BD thay đổi. Giá trị lớn nhất của thể tích khối tứ diện ABCD bằng.
A. 2 3 27
B. 4 3 27
C. 2 3 9
D. 4 3 9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

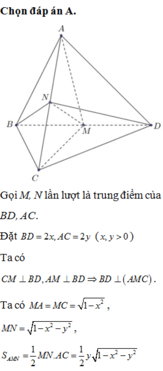
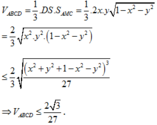

Chọn A
Gọi M, N lần lượt là trung điểm của BD, AC. Đặt BD = 2x, AC = 2y (x, y > 0).
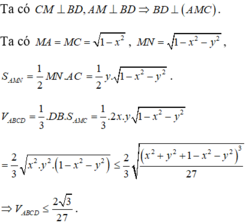

Chọn B

Gọi M, N lần lượt là trung điểm AD và BC.
Theo giả thiết ta có: ABD và ACD là các tam giác cân có M là trung điểm của AD nên:
![]()
Và có BM=CM => ΔMBC cân tại M
Trong tam giác ΔMBC có MN vừa là đường cao vừa là trung tuyến nên

Khi đó diện tích tam giác ΔMBC là:

Thể tích tứ diện ABCD là:

Đặt AD=x, BC=y ta có:

Dấu bằng xảy ra khi x=y.
Ta lại có:

Dấu bằng xảy ra khi:

Vậy giá trị lớn nhất của thể tích khối tứ diện ABCD là:


Đáp án A
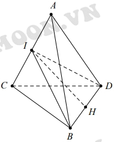 Gọi I, H lần lượt là trung điểm AC, BD. Ta có
B
I
⊥
A
C
D
I
⊥
A
C
⇒
A
C
⊥
I
B
D
và
V
I
.
B
C
D
=
V
I
.
A
B
D
Gọi I, H lần lượt là trung điểm AC, BD. Ta có
B
I
⊥
A
C
D
I
⊥
A
C
⇒
A
C
⊥
I
B
D
và
V
I
.
B
C
D
=
V
I
.
A
B
D
Lại có I B = A B 2 - A I 2 = 1 - x 2 4 ,với AC = BD = x.
Và I H = I B 2 - B H 2 = 1 - x 2 4 - x 2 4 = 1 - x 2 2
Diện tích tam giác IBD là S ∆ I B D = 1 2 I H . B D = x 2 1 - x 2 2
Suy ra V A B C D = 2 V I . B C D = 2 3 I C . S I B D = x 3 . x 2 1 - x 2 2 = x 2 6 1 - x 2 2
Xét hàm số f x = x 2 2 - x 2 → m a x f x = 4 6 9
Vậy thể tích lớn nhất là V m a x = 4 6 9 : 6 2 = 2 3 27

Đáp án C
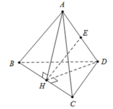
Gọi H là trung điểm BC khi đó A H ⊥ B C D H ⊥ B C
SUY RA B C ⊥ A H D và ta có A H = D H = a 3 2
Gọi E là trung điểm của AD do tam giác AHD cân nên
H E ⊥ A D ⇒ H E = A H 2 − A E 2 = 3 a 2 4 − x 2 4
Ta có V A B C D = V B A H D + V C A H D = 1 3 B C . S A H D = 1 3 a 1 2 H E . A D
Lại có
3 a 2 4 − x 2 4 . x = 2. 3 a 2 4 − x 2 4 . x 2 ≤ 3 a 2 4 − x 2 4 + x 2 4 = 3 a 2 4 ⇒ V A B C D ≤ a 3 8 ⇒ V m a x = a 3 8
Dấu bằng xảy ra khi và chỉ khi 3 a 2 = 2 x 2 ⇔ x = a 6 2 = 3 2

Đáp án B
Đặt a=2. Gọi H là trung điểm của BC khi đó A H ⊥ B C D H ⊥ B C
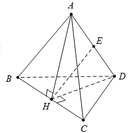
Suy ra B C ⊥ A H D và ta có A H = D H = a 3 2
Gọi E là trung điểm của AD do tam giác AHD cân nên
H E ⊥ A D ⇒ H E = A H 2 − A E 2 = 3 a 2 4 − x 2 4
Ta có V A B C D = V B . A H D + V C . A H D
= 1 3 B C . S A H D = 1 3 a . 1 2 H E . A D
Lại có:
3 a 2 4 − x 2 4 . x = 2 3 a 2 4 − x 2 4 . x 2 ≤ 3 a 2 4 − x 2 4 + x 2 4
= 3 a 2 4 ⇒ V A B C D ≤ a 3 8 ⇒ V max = a 3 8 .
Dấu bằng xảy ra 3 a 2 = 2 x 2 ⇔ x = a 6 2 = 6
Cách 2: Nhận xét V max ⇔ S A H D lớn nhất 1 2 A H . D H sin A H D ⏜ = 3 a 2 8 . sin A H D ⏜ ≤ 3 a 2 8