Chọn ngẫu nhiên 3 đỉnh của một đa giác đều 20 đỉnh. Xác suất để chọn được 3 đỉnh lập thành một tam giác nhọn bằng
A. 6 19
B. 4 19
C. 3 19
D. 9 19
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 3 2019
Đáp án B
Số cách chọn ngẫu nhiên 3 đỉnh là C 20 3
Số cách chọn ra 3 đỉnh là 3 đỉnh của tam giác vuông là 10 C 18 1
Số cách chọn ra 3 đỉnh là 3 đỉnh của tam giác tù là
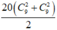
Số cách chọn ra 3 đỉnh là 3 đỉnh của tam giác nhọn là
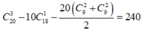
Xác suất cần tính bằng 240 C 20 3 = 4 19
H
4 tháng 4 2021
Số tam giác tạo ra từ 18 đỉnh là :
\(C^3_{18}=816\)
Với 1 đỉnh , ta kẻ đường kính từ đỉnh đó đi qua tâm đa giác đều, thì mỗi cặp điểm nằm đối xứng qua đường kính đó ghép với đỉnh kia tạo thành tam giác cân.
Mà có tất cả 8 cặp đó
=> Với 1 đỉnh tạo được 8 tam giác cân
Với 18 đỉnh tạo được 144 tam giác cân.
Nhưng trong 18 đỉnh của đa giác đều , tạo được \(\dfrac{18}{3}=6\)
tam giác đều. Mà mỗi tam giác đều là cân tại 3 đỉnh
Vậy nên 6 tam giác đều đó được lặp lại 3 lần, thừa 2 lần.
Vậy số tam giác cân thực tế là : 144 - 6 x 2=132
Xác suất là \(P=\dfrac{132}{816}=\dfrac{11}{68}\)
CM
4 tháng 4 2019
Chọn C.
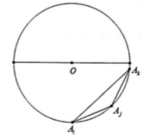
Gọi đa giác đều là A1A2..A100 và O là tâm đường tròn ngoại tiếp tam giác đã cho.
Chọn 3 điểm bất kì ta được 1 tam giác suy ra có: C 100 3 tam giác.
Chia 100 đỉnh thành 2 phần thuộc 2 nửa đường tròn khác nhau
Bước 1: Chọn 1 đỉnh có 100 cách chọn.
Bước 2: Chọn 2 đỉnh còn lại để tạo thành 3 đỉnh của tam giác AiAjAk tù thì 2 đỉnh này phải nằm trên 1 nửa đường trò đã chia.
Như vậy có: 100 . C 49 2 cách chọn.
Do đó xác xuất cần tìm là: 100 . C 49 2 C 100 2 = 8 11
CM
8 tháng 6 2019
Đáp án C
Gọi đường tròn (O) là đường tròn ngoại tiếp đa giác. Xét A là 1 đỉnh bất kỳ của đa giác,kẻ đường kính AA’ thì A’ cũng là 1 đỉnh của đa giác. Đường kính AA’ chia (O) thành 2 nửa đường tròn , với mỗi cách chọn ra 2 điểm B và C là 2 đỉnh của đa giác và cùng thuộc 1 nửa đường tròn, ta đường 1 tam giác tù ABC. Khi đó số cách chọn B và C là: 2 C 49 2
Đa giác có 100 đỉnh nên số đường chéo là đường kính của đường tròn ngoại tiếp đa giác là 50
Do đó, số cách chọn ra 3 đỉnh để lập thành 1 tam giác tù là: 
Không gian mẫu: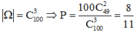 
CM
26 tháng 4 2017
Đáp án C
Gọi đường tròn (O) là đường tròn ngoại tiếp đa giác. Xét A là 1 đỉnh bất kỳ của đa giác,kẻ đường kính AA’ thì A’ cũng là 1 đỉnh của đa giác. Đường kính AA’ chia (O) thành 2 nửa đường tròn , với mỗi cách chọn ra 2 điểm B và C là 2 đỉnh của đa giác và cùng thuộc 1 nửa đường tròn, ta đường 1 tam giác tù ABC. Khi đó số cách chọn B và C là: 2 C 49 2
Đa giác có 100 đỉnh nên số đường chéo là đường kính của đường tròn ngoại tiếp đa giác là 50
Do đó, số cách chọn ra 3 đỉnh để lập thành 1 tam giác tù là: 50 . 2 C 49 2 = 100 C 49 2
Không gian mẫu:
CM
7 tháng 6 2019
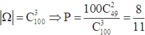
Chọn D.
Chọn ngẫu nhiên 3 đỉnh trong 14 đỉnh của đa giác => có C 14 3 = 364 cách.
Suy ra số phần tử của không gian mẫu là n Ω = 364 .
Gọi X là biến cố “3 đỉnh được chọn là 3 đỉnh của một tam giác vuông”
Gọi O là tâm đường tròn ngoại tiếp đa giác đều => có 7 đường kính đi qua O.
Xét một đường kính bất kì, mỗi đỉnh còn lại sẽ tạo với đường kính một tam giác vuông.
Khi đó, số tam giác vuông được tạo ra là 7.(6+6)=84=>n(X)=84.
Vậy xác suất cần tính là
8 tháng 4 2023
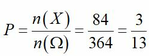
SỐ tam giác tạo được từ 3 đỉnh là \(C^3_{12}\)
Số tam giác có 3 đỉnh là 3 đỉnh của đa giác và 2 cạnh là cạnh của đa giác: cứ 3 đỉnh liên tiếp cho 1 tam giác thỏa mãn
=>Có 12 tam giác
Số tam giác có 3 đỉnh là đỉnh của đa giác và 1 cạnh là cạnh của đa giác
=>CÓ 8*12=96 tam giác
=>\(P=\dfrac{C^3_{12}-12-12\cdot8}{C^3_{12}}\)
Đáp án đúng : B