Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt cầu S 1 : x 2 + y 2 + z 2 + 4 a + 2 y + z = 0 và S 2 : x 2 + y 2 - 2 x - y - z = 0 cắt nhau theo một đường tròn (C) nằm trong mặt phẳng (P). Cho các điểm A(1;0;0), B(0;2;0), C(0;0;3). Có bao nhiêu mặt cầu tâm thuộc (P) và tiếp xúc với ba đường thẳng AB, BC, CA?
A. 4 mặt cầu
B. 2 mặt cầu
C. 3 mặt cầu
D. 1 mặt cầu

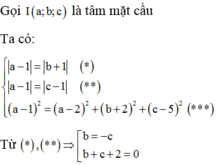
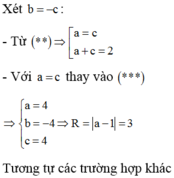





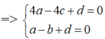
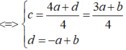
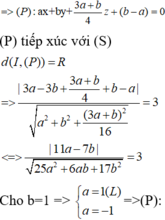
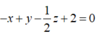

Chọn đáp án A
Ta có C = S 1 ∩ S 2
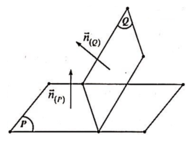
⇒ Mặt phẳng (P) chứa đường tròn (C) có phương trình thỏa mãn
Phương trình mặt phẳng (ABC) là:
Suy ra (P) // (Q)
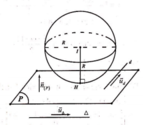
Mặt cầu (S) tiếp xúc với ba đường thẳng AB, BC, CA sẽ giao với mặt phẳng (ABC) theo một đường tròn tiếp xúc với ba đường thẳng AB, BC, CA.
Trên mặt phẳng (ABC) có 4 đường tròn tiếp xúc với ba đường thẳng AB, BC, CA; đó là đường tròn nội tiếp tam giác ABC và ba đường tròn bàng tiếp các góc A, B, C. Do đó có 4 mặt cầu, tâm nằm trên mặt phẳng (P) và tiếp xúc với cả ba đường thẳng AB, BC, CA
Tâm của 4 mặt cầu này là hình chiếu của tâm 4 đường tròn tiếp xúc với ba đường thẳng AB, BC, CA lên mặt phẳng (P).