Cho hình lập phương ABCD.A' B'C' D' cạnh bằng a và K là một điểm nằm trên cạnh CC’ sao cho C K = 2 a 3 . Mặt phẳng α qua A, K và song song với BD chia khối lập phương thành hai phần có thể tích V 1 , V 2 V 1 < V 2 . Tính tỉ số V 1 V 2
A. V 1 V 2 = 1 4
B. V 1 V 2 = 1 2
C. V 1 V 2 = 2 3
D. V 1 V 2 = 1 3

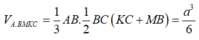
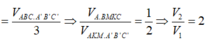









Đáp án B
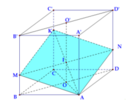
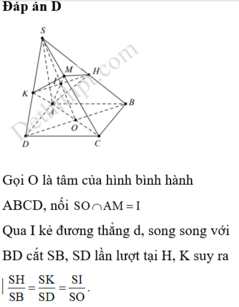
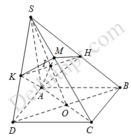
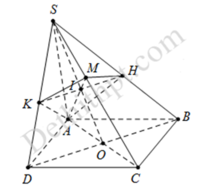
Gọi tâm O, O’ lần lượt là tâm của ABCD, A’B’C’D’. Ta có I = A K ∩ O O '
Qua I ta kẻ đường thẳng d song song BD cắt BB', DD' lần lượt tại M, N . Mặt phẳng α chính là mặt phẳng (KMAN) chia khối lập phương thành 2 phần.
Ta có 2 phần khối đa diện đối xứng qua (AA'C'C) nên ta chỉ cần xét một nửa thể tích của mỗi phần như sau: