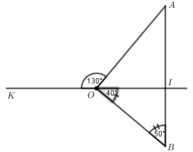
Hình bên hai tia OI, OK đối nhau. Tia OI cắt đoạn thẳng AB tại I. Biết K O A ^ = 130 ∘ , B O I ^ = 40 ∘ , O B I ^ = 50 ∘ . Tính K O B ^ , A O I ^ , B O A ^ .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

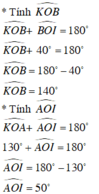
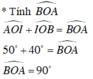

Vì ∠(KOB) và ∠(BOI) kề bù nên ∠(KOB) + ∠(BOI) = 180o
Suy ra: ∠(KOB) = 180o - ∠(BOI) = 180o – 45o = 135o
Vì ∠(KOA) và ∠(AOI) kề bù nên ∠(KOA) + ∠(AOI) = 180o
Suy ra: ∠(AOI) = 180 - ∠(KOA) = 180o – 120o = 60o
Vì tia OI nằm giữa hai tia OA và OB nên:
∠(AOI) + ∠(BOI) = ∠(AOB)
Suy ra : ∠(AOB) = 60o + 45o = 105o


\(\widehat{KOB}=60^o.\)
\(\widehat{AOI}=60^o.\)
\(\widehat{BOA}=180^o.\)
+) Vì góc KOB và BOI là 2 góc kề bù nên
KOB=180-45=135 độ
+) Vì góc AOI và KOA là 2 góc kề bù nên
AOI=180-120=60 độ
+) Vì tia OI nằm giữa 2 tia OA và OB nên
BOI+AOI=BOA
45+60=BOA
BOA=45+60
BOA=105
Vậy góc KOB=135,AOI=60,BOA=105


a, Chỉ ra |OI – OK| < IK < OI + OK => (1) và (k) luôn cắt nhau
b, Do OI=NK, OK=IM => OM=ON
Mặt khác OMCN là hình chữ nhật => OMCN là hình vuông
c, Gọi{L} = KB ∩ MC, {P} = IBNC => OKBI là Hình chữ nhật và BNMI là hình vuông
=> ∆BLC = ∆KOI
=> L B C ^ = O K I ^ = B I K ^
mà B I K ^ + I B A ^ = 90 0
L B C ^ + L B I ^ + I B A ^ = 180 0
d, Có OMCN là hình vuông cạnh a cố định
=> C cố định và AB luôn đi qua điểm C