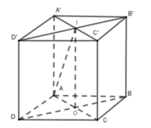
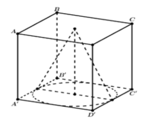
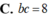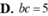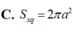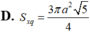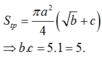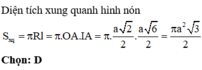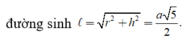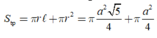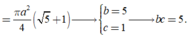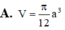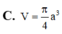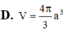Cho hình lập phương ABCDA'B'C'D' có cạnh a. Một hình nón có đỉnh là tâm của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuông A'B'C'D'. Kết quả diện tích toàn phần S t p của hình nón đó bằng πa 2 4 b + c với b và c là hai số nguyên dương và b>1. Tính bc.
![]()
![]()