Để đường thẳng d: y=2x+m cắt đồ thị hàm số ( C ) : 2 x - 2 x + 1 tại hai điểm phân biệt A, B sao cho A B = 5 thì giá trị dương của m là
A. −3.
B. 2
C. 10.
D. 4.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


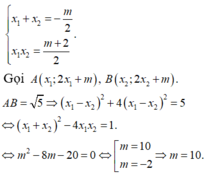

Phương trình hoành độ giao điểm: m x - 1 x + 2 = 2 x - 1 ( 1 )
Điều kiện: x ≠ - 2 Khi đó
(1) Suy ra: mx-1=(2x-1) (x+2) hay 2x2-(m-3)x-1=0 (2)
Đường thẳng d cắt (C) tại hai điểm phân biệt A; B khi và chỉ khi (1) có hai nghiệm phân biệt khi và chỉ khi ( 2) có hai nghiệm phân biệt khác -2
⇔ ∆ = [ - ( m - 3 ) ] 2 + 8 > 0 8 + 2 m - 6 - 1 ≠ 0 ⇔ m ≠ - 1 2 ( * )
Đặt A( x1; 2x1-1); B( x2; 2x2-1) với x1; x2 là hai nghiệm của phương trình (2).
Theo định lý Viet ta có
x 1 + x 2 = m - 3 2 x 1 x 2 = - 1 2 , k h i đ ó
A B = ( x 1 - x 2 ) 2 + 4 ( x 1 - x 2 ) 2 = 10 ⇔ 5 [ ( x 1 + x 2 ) 2 - 4 x 1 x 2 ] = 10 ⇔ ( m - 3 2 ) 2 + 2 = 2 ⇔ m = 3
thỏa (*).
Vậy giá trị m cần tìm là m =3.

Phương trình hoành độ giao điểm của (C) và d là:
x + 1 x - 1 = 2 x + m ⇔ x ≠ 1 f x = 2 x 2 + m - 3 - m - 1
Ta có
∆ = m 2 + 2 m + 7 > 0 ∀ m f 1 = - 2 ≠ 0
=> d luôn cắt ![]() tại hai điểm phân biệt A, B.
tại hai điểm phân biệt A, B.
Gọi x 1 ; x 2 lần lượt là hoành độ các điểm A, B. Khi đó A O B ⏞ nhọn.
⇔ cos A O B ⏞ = O A 2 + O B 2 - A B 2 2 . O A . O B > 0 ⇔ O A 2 + O B 2 > A B 2 ⇔ x 1 2 + 2 x 1 + m 2 + x 2 2 + 2 x 2 + m 2 > 5 x 2 - x 1 2
Sử dụng định lí Viet và giải bất phương trình theo m ta thu được m > 5
Đáp án C

Chọn C.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d
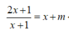
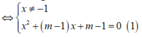
Khi đó d cắt (C) tại hai điểm phân biệt A, B khi và chỉ khi phương trình (1) có hai nghiệm phân biệt khác -1
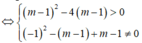
![]()
Ta có
![]()
![]()
![]()
Và 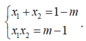
Từ đây ta có
![]()
![]()
![]()
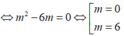 ( thỏa mãn *)
( thỏa mãn *)
Vậy chọn m = 0 hoặc m = 6

Chọn C.
Phương pháp: Sử dụng phương trình hoành độ giao điểm và định lý Viet.
Cách giải: Phương trình hoành độ giao điểm là

Vì a,c là nghiệm của (*) nên theo định lý Viet ta có:
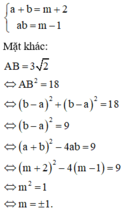

Đáp án C
Xét pt tương giao:
2 x - 1 x - 1 = x + m ⇔ 2 x - 1 - x + m x - 1 = 0 ⇔ x 2 - 3 - m x + m - 1 = 0
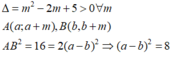
a + b 2 - 4 a b = 8 ⇔ 3 - m 2 - 4 1 - m = 8 ⇔ [ m = - 1 m = 3