Một máy quang phổ có lăng kính thuỷ tinh góc chiết quang 40 ° . Chiếu đồng thời bức xạ màu lục và màu tím vào máy quang phổ. Biết chiết suất của chất làm lăng kính đối với bức xạ màu tím là 1,635. Lăng kính được đặt sao cho bức xạ tím cho góc lệch cực tiểu. Tính góc tới của chùm sáng tới lăng kính.
A. 47 , 9 °
B. 39 °
C. 45 , 9 °
D. 34 °


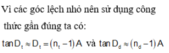
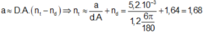
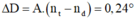
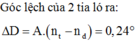
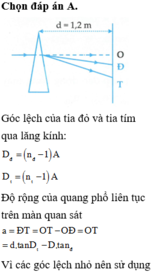

Chọn D
sin i 1 = sin D min + A 2 = n sin A 2 ⇒ sin i 1 = 1 , 635 sin 40 ° 2 ⇒ i 1 = 34 °