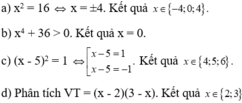Tìm x, biết: 2 x x – 5 + 5 x – 5 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

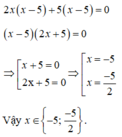

a: \(\Leftrightarrow\left(x+2\right)\left(x+2-2x+10\right)=0\)
\(\Leftrightarrow x\in\left\{-2;12\right\}\)

Lời giải:
1. $|x-1|-|5-x|=0$
$\Leftrightarrow |x-1|=|5-x|$
$\Leftrightarrow x-1=5-x$ hoặc $x-1=x-5$
$\Leftrightarrow x=3$ hoặc $1=5$ (vô lý)
Vậy $x=3$
---------------------------
2.
Nếu $x\geq 4$ thì pt trở thành:
$x-4+x-\frac{3}{2}=5$
$\Leftrightarrow x=5,25$ (thỏa mãn)
Nếu $\frac{3}{2}\leq x< 4$ thì:
$4-x+x-\frac{3}{2}=5\Leftrightarrow \frac{5}{2}=5$ (vô lý)
Nếu $x< \frac{3}{2}$ thì:
$4-x+\frac{3}{2}-x=5$
$\Leftrightarrow x=0,25$ (thỏa mãn)

\(2x^2-7x+5=0\)
\(2x^2-2x-5x+5=0\)
\(2x\left(x-1\right)-5\left(x-1\right)=0\)
\(\left(x-1\right)\left(2x-5\right)=0\)
\(\left[\begin{array}{nghiempt}x-1=0\\2x-5=0\end{array}\right.\)
\(\left[\begin{array}{nghiempt}x=1\\2x=5\end{array}\right.\)
\(\left[\begin{array}{nghiempt}x=1\\x=\frac{5}{2}\end{array}\right.\)
\(x\left(2x-5\right)-4x+10=0\)
\(x\left(2x-5\right)-2\left(2x-5\right)=0\)
\(\left(2x-5\right)\left(x-2\right)=0\)
\(\left[\begin{array}{nghiempt}x-2=0\\2x-5=0\end{array}\right.\)
\(\left[\begin{array}{nghiempt}x=2\\2x=5\end{array}\right.\)
\(\left[\begin{array}{nghiempt}x=2\\x=\frac{5}{2}\end{array}\right.\)
\(\left(x-5\right)\left(x+5\right)-x\left(x-2\right)=15\)
\(x^2-25-x^2+2x=15\)
\(2x=15+25\)
\(2x=40\)
\(x=\frac{40}{2}\)
\(x=20\)
\(x^2\left(2x-3\right)-12+8x=0\)
\(x^2\left(2x-3\right)+4\left(2x-3\right)=0\)
\(\left(2x-3\right)\left(x^2+4\right)=0\)
\(2x-3=0\) (vì \(x^2\ge0\Rightarrow x^2+4\ge4>0\))
\(2x=3\)
\(x=\frac{3}{2}\)
\(x\left(x-1\right)+5x-5=0\)
\(x\left(x-1\right)+5\left(x-1\right)=0\)
\(\left(x-1\right)\left(x+5\right)=0\)
\(\left[\begin{array}{nghiempt}x-1=0\\x+5=0\end{array}\right.\)
\(\left[\begin{array}{nghiempt}x=1\\x=-5\end{array}\right.\)
\(\left(2x-3\right)^2-4x\left(x-1\right)=5\)
\(4x^2-12x+9-4x^2+4x=5\)
\(-8x=5-9\)
\(-8x=-4\)
\(x=\frac{4}{8}\)
\(x=\frac{1}{2}\)
\(x\left(5-2x\right)+2x\left(x-1\right)=13\)
\(5x-2x^2+2x^2-2x=13\)
\(3x=13\)
\(x=\frac{13}{3}\)
\(2\left(x+5\right)\left(2x-5\right)+\left(x-1\right)\left(5-2x\right)=0\)
\(\left(2x+10\right)\left(2x-5\right)-\left(x-1\right)\left(2x-5\right)=0\)
\(\left(2x-5\right)\left(2x+10-x+1\right)=0\)
\(\left(2x-5\right)\left(x+11\right)=0\)
\(\left[\begin{array}{nghiempt}2x-5=0\\x+11=0\end{array}\right.\)
\(\left[\begin{array}{nghiempt}2x=5\\x=-11\end{array}\right.\)
\(\left[\begin{array}{nghiempt}x=\frac{5}{2}\\x=-11\end{array}\right.\)

cậu cho mk xin link facebook của jonathan galindo đi rồi mk sẽ trả lời câu hỏi của cậu

a, => x^2+5 = 0
=> x^2=-5 ( vô lí vì x^2 >= 0)
=> ko tồn tại x tm bài toán
b, Vì x^2-5 > x^2-25
Mà (x^2-5): (x^2-25) < 0
=> x^2-5 >0 và x^2-25 <0
=> 5 < x^2 < 25
=> \(x>\sqrt{5}\)hoặc \(x< -\sqrt{5}\) và -5 < x < 5
=> -5 < x < -\(\sqrt{5}\)hoặc \(\sqrt{5}\)< x < 5
k mk nha

\(\left(x^2-5\right)\left(x^2+1\right)=0\)
<=> \(\hept{\begin{cases}x^2-5=0\\x^2+1=0\end{cases}}\)
<=> \(\hept{\begin{cases}x^2=5\\x^2=-1\end{cases}}\)
<=> \(\hept{\begin{cases}x=\sqrt{5};x=-\sqrt{5}\\x\in\varnothing\end{cases}}\)
câu còn lại tương tự nha

1.
a)\(0< x-1\le2\)
Mà \(x\in Z\)
\(\Rightarrow x-1\in Z\)
\(\Rightarrow x-1=1\)
\(\Rightarrow x=2\in Z\)
Vậy x=2
Các phần khác bn làm tương tự nha
d)\(\left|x\right|< 3\)
\(\Rightarrow-3< x< 3\)
\(\Rightarrow x\in\left\{-2;-1;0;1;2\right\}\)
Vậy \(x\in\left\{-2;-1;0;1;2\right\}\)
2.
c)Các phần a,b bn tự làm nha
3-|2x+1|=(-5)
\(\Rightarrow\left|2x+1\right|=3-\left(-5\right)\)
\(\Rightarrow\left|2x+1\right|=3+5\)
\(\Rightarrow\left|2x+1\right|=8\)
\(\Rightarrow2x+1=8\) hoặc \(2x+1=-8\)
\(\Rightarrow2x=8-1\) \(\Rightarrow2x=-8-1\)
\(\Rightarrow2x=7\) \(\Rightarrow2x=-9\)
\(\Rightarrow x=\frac{7}{2}=3,5\notin Z\) \(\Rightarrow x=\frac{-9}{2}=-4,5\in Z\)
Vậy \(x\in\varnothing\)
Chúc bn học tốt