Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Gọi số có 4 chữ số có dạng 
(a, b, c, d là các chữ số, 
).
Số phần tử của không gian mẫu 
Gọi A là biến cố “Chọn được số lớn hơn 2500”.
Trường hợp 1: 
Chọn a: từ 3, 4,…, 9 → có 7 cách chọn.
Chọn b: khác a → có 9 cách chọn.
Chọn c: khác a, b → có 8 cách chọn.
Chọn d: khác a, b, c → có 7 cách chọn.
Vậy trường hợp này có 
số.
Trường hợp 2: 
Chọn a: 
→ có 1 cách chọn.
Chọn b: từ 6, 7, 8, 9 → có 4 cách chọn.
Chọn c: khác a, b → có 8 cách chọn.
Chọn d: khác a, b, c → có 7 cách chọn.
Vậy trường hợp này có 
số.
Trường hợp 3: 
Chọn a: 
→ có 1 cách chọn.
Chọn b: 
→ có 1 cách chọn.
Chọn c: từ 1, 3, 4, 6, 7, 8, 9 → có 7 cách chọn.
Chọn d: khác a, b, c → có 7 cách chọn.
Vậy trường hợp này có 
số.
Trường hợp 4: 
Chọn a: 
→ có 1 cách chọn.
Chọn b: 
→ có 1 cách chọn.
Chọn c: 
→ có 1 cách chọn.
Chọn d: từ 1, 3, 4, 6, 7, 8, 9 → có 7 cách chọn.
Vậy trường hợp này có 
số.
Như vậy
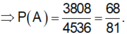
n(S)=6!
Để thỏa mãn yêu cầu đề bài thì cần chọn ra 3 số có tổng là 12
=>Số trường hợp thỏa mãn là (1;5;6); (2;4;6); (3;4;5)
=>Có 3*3!*3!
=>P=3/20
Gọi chữ số cuối là x thì tổng 4 chữ số đầu là \(x+2\)
\(\Rightarrow\) Tổng 5 chữ số là: \(2x+2\)
Mặt khác tổng 5 chữ số nhỏ nhất từ tập đã cho là \(1+2+3+4+5=15\)
\(\Rightarrow2x+2\ge15\Rightarrow2x\ge13\)
\(\Rightarrow x=\left\{7;8;9\right\}\)
TH1: \(x=7\Rightarrow\) tổng 4 chữ số đầu là 9 mà \(1+2+3+4>9\Rightarrow\) không tồn tại 4 chữ số thỏa mãn
TH2: \(x=8\Rightarrow\) tổng 4 chữ số đầu bằng 10
Trong 9 chữ số, chỉ có duy nhất bộ \(\left\{1;2;3;4\right\}\) có tổng bằng 10
Do đó số số trong trường hợp này là: \(4!\) số
TH3: \(x=9\Rightarrow\) tổng 4 chữ số đầu bằng \(11\Rightarrow\) có 1 bộ 4 chữ số thỏa mãn là \(\left\{1;2;3;5\right\}\)
Trường hợp này cũng có \(4!\) số
Xác suất: \(P=\dfrac{4!+4!}{A_9^5}=...\)
Chọn A
Gọi số tự nhiên có bốn chữ số thỏa mãn yêu cầu bài toán là 
Số phần tử của không gian mẫu là 
Gọi biến cố A ‘‘Số được chọn lớn hơn số 6700’’.
Ta các TH sau:
TH1: có 1 cách chọn.
có 3 cách chọn.
+ Các chữ số c,d được chọn từ 8 chữ số còn lại có sắp thứ tự và số cách chọn là A 8 2
Số cách để chọn ở trường hợp 1 là: 3. A 8 2
TH2 : 
có 3 cách chọn. Khi đó: b,c,d có
A
9
3
cách chọn.
Số cách để chọn ở trường hợp 1 là: 3. A 9 3
Như vậy, ta được n(A) = 3. A 8 2 + 3. A 9 3 = 1680
Suy ra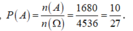 
Gọi số đó là \(\overline{abcdef}\Rightarrow a+b+c+d+e+f=1+2+3+4+5+6=21\)
Mặt khác \(a+b+c=d+e+f-1\)
\(\Rightarrow\left\{{}\begin{matrix}a+b+c=10\\d+e+f=11\end{matrix}\right.\)
\(\Rightarrow\left(a;b;c\right)=\left(1;3;6\right);\left(1;4;5\right);\left(2;3;5\right)\)
Số số thỏa mãn: \(3.\left(3!.3!\right)=108\)
Xác suất: \(P=\dfrac{108}{6!}=\dfrac{3}{20}\)
Số phần tử của S là: \(8!\)
Gọi tổng 4 chữ số sau là S \(\Rightarrow\) tổng 4 chữ số đầu là \(S+2\)
Ta có: \(S+S+2=1+3+4+5+6+7+8+9\)
\(\Rightarrow2S=41\Rightarrow S=\dfrac{41}{2}\) (vô lý do các chữ số đều nguyên)
Vậy đề bài sai
Đáp án C
Gọi số có 4 chữ số có dạng abcd ¯ (a, b, c, d là các chữ số, a ≠ 0 ).
Số phần tử của không gian mẫu n(S) = 9.9.8.7 = 4536
Gọi A là biến cố “Chọn được số lớn hơn 2500”.
Chọn a: từ 3, 4,…, 9 → có 7 cách chọn.
Chọn b: khác a → có 9 cách chọn.
Chọn c: khác a, b → có 8 cách chọn.
Chọn d: khác a, b, c → có 7 cách chọn.
Vậy trường hợp này có 7.9.8.7 = 3528 số.
Chọn a: a = 2 → có 1 cách chọn.
Chọn b: từ 6, 7, 8, 9 → có 4 cách chọn.
Chọn c: khác a, b → có 8 cách chọn.
Chọn d: khác a, b, c → có 7 cách chọn.
Vậy trường hợp này có 1.4.8.7 = 224 số.
Chọn a: a = 2 → có 1 cách chọn.
Chọn b: b = 5 → có 1 cách chọn.
Chọn c: từ 1, 3, 4, 6, 7, 8, 9 → có 7 cách chọn.
Chọn d: khác a, b, c → có 7 cách chọn.
Vậy trường hợp này có 1.1.7.7 = 49 số.
Chọn a: a = 2 → có 1 cách chọn.
Chọn b: b = 5 → có 1 cách chọn.
Chọn c: c = 0 → có 1 cách chọn.
Chọn d: từ 1, 3, 4, 6, 7, 8, 9 → có 7 cách chọn.
Vậy trường hợp này có 1.1.1.7 = 7 số.
Như vậy n A = 3528 + 224 + 49 + 7 = 3808 ⇒ P A = 3808 4536 = 68 81 .