Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng 1. Gọi M, N lần lượt là trung điểm của AB và CD. Tính khoảng cách giữa hai đường thẳng A'C và MN.
A. 2 2
B. 2 4
C. 2 2
D. 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 5 2017
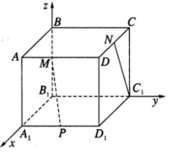
Ta chọn hệ trục tọa độ như sau: B 1 là gốc tọa độ, B 1 A 1 → = i → , B 1 C 1 → = j → , B 1 B → = k → . Trong hệ trục vừa chọn, ta có B 1 (0; 0; 0), B(0; 0; 1), A 1 (1; 0; 0), D 1 (1; 1; 0), C(0; 1; 1), D(1; 1; 1), C 1 (0; 1; 0).
Suy ra M(0; 0; 1/2), P(1; 1/2; 0), N(1/2; 1; 1)
Ta có MP → = (1; 1/2; −1/2); C 1 N → = (1/2; 0; 1)
Gọi ( α ) là mặt phẳng chứa C 1 N và song song với MP. ( α ) có vecto pháp tuyến là n → = (1/2; −5/4; −14) hay n ' → = (2; −5; −1)
Phương trình của ( α ) là 2x – 5(y – 1) – z = 0 hay 2x – 5y – z + 5 = 0
Ta có:
d(MP,
C
1
N) = d(M,(
α
)) 
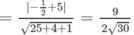
Ta có:
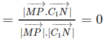
Vậy ∠ (MP, C 1 N) = 90 ° .
CM
13 tháng 3 2017
Chọn D.
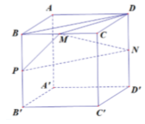
Gọi P là trung điểm BB’. Ta có BD//PN => BD//(MPN). Do đó:
d(MN;BD) = d(BD;(MPN)) = d(B;(MPN))
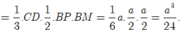
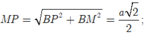
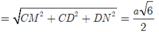
Nhận thấy 
nên tam giác MPN vuông tại M.
Do đó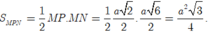 
Ta có 
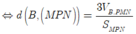
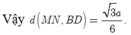
Cách 2:
Gọi P là trung điểm BB’. Ta có BD//PN => BD//(MPN).
Đồng thời, MP//CB', PN//B'D' => (MPN)//(CB'D')
Do đó 
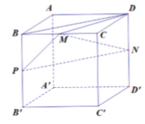
(vì PC’ cắt B’C tại trọng tâm tam giác BB’C’).
Nhận thấy tứ diện C'.CB'D' là tứ diện vuông tại C' nên
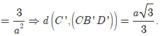
Vậy 
Cách 3: Tọa độ hóa
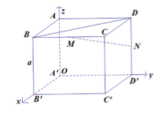
Chọn hệ trục tọa độ Oxyz như hình vẽ. Khi đó,
CM
28 tháng 8 2019
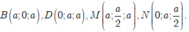
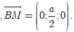
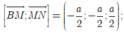
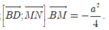
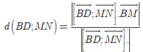
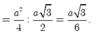
Đáp án D.
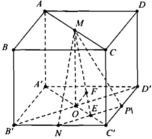
Gọi P là trung điểm của C’D’ suy ra d = d O ; M N P
Dựng:
O A ⊥ N P ; OF ⊥ ME ⇒ d=OF= M O . N E M O 2 + N E 2
trong đó
M O = a ; N E = a 2 4 ⇒ d = a 3 .
Chọn B.
Phương pháp: Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách từ một trong hai đường thẳng đó tới mặt phẳng chứa đường thẳng kia và song song với nó.
Khoảng cách giữa đường thẳng và mặt phẳng song song với nhau là khoảng cách từ điểm bất kỳ trên đường thẳng tới mặt phẳng đó.