Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
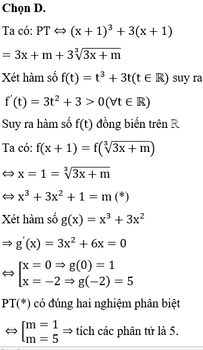
Đáp án D.
ta có m 4 − m 2 + 1 = m 2 − 1 2 2 + 3 4 ≥ 3 4 ∀ m
1 5 x 2 − 4 x + 3 = m 4 − m 2 + 1 ⇔ x 2 − 4 x + 3 = − log 4 m 4 − m 2 + 1
Xét hàm số y = x 2 − 4 x + 3 có bảng biến thiên:
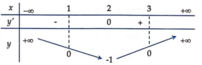
Suy ra bảng biến thiên của hàm số y = x 2 − 4 x + 3 :
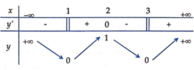
Phương trình x 2 − 4 x + 3 = − log 5 m 4 − m 2 + 1 có 4 nghiệm phân biệt
⇔ 0 < − log 5 m 4 − m 2 + 1 < 1 ⇔ − 1 < log 5 m 4 − m 2 + 1 < 0
⇔ 1 5 < m 4 − m 2 + 1 < 1 ⇔ m 4 − m 2 + 1 < 1
( do m 4 − m 2 + 1 ≥ 3 4 > 1 5 )
⇔ m 4 − m 2 < 0 ⇔ m 2 m 2 − 1 < 0 ⇔ m ≠ 0 m 2 − 1 < 0 ⇔ m ≠ 0 − 1 < m < 1
⇔ m ∈ − 1 ; 0 ∪ 0 ; 1
Vậy S = − 1 ; 0 ∪ 0 ; 1 , tức là S là hợp của hai khoảng với nhau. Vậy D là đáp án đúng.
Lời giải:
Đặt $\sqrt{x+2}=t(t\geq 0)$ thì pt trở thành:
$t^2-2-2t-m-3=0$
$\Leftrightarrow t^2-2t-(m+5)=0(*)$
Để PT ban đầu có 2 nghiệm pb thì PT $(*)$ có 2 nghiệm không âm phân biệt.
Điều này xảy ra khi \(\left\{\begin{matrix} \Delta'=1+m+5>0\\ S=2>0\\ P=-(m+5)\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m>-6\\ m\leq -5\end{matrix}\right.\)
Đáp án B.
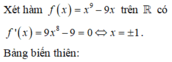
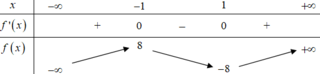
Từ bảng biến thiên ta thấy, phương trình đã cho có đúng hai nghiệm
Đáp án C.
Đặt t = sin x , t ∈ − 1 ; 1 . Phương trình đã cho trở thành 2 t + 1 t + 2 = m (*).
Để phương trình đã cho có đúng hai nghiệm thuộc đoạn 0 ; π thì phương trình (*) phải có đúng một nghiệm thuộc nửa khoảng 0 ; 1 .
Xét hàm số f t = 2 t + 1 t + 2 . Ta có f ' t = 3 t + 2 2 .
Bảng biến thiên của :
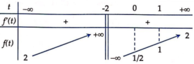
Vậy để phương trình (*) có đúng một nghiệm thuộc nửa khoảng 0 ; 1 thì m ∈ 1 2 ; 1 . Vậy C là đáp án đúng
