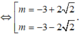Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
A ∈ y ⇒ A ( x ; x 3 − 3 x 2 − x + 2 ) d ( A ; Ox)=d(A;Oy) ⇒ x 3 − 3 x 2 − x + 2 = x x 3 − 3 x 2 − x + 2 = − x
Giải hai pt trên ta thấy mỗi pt có 3 nghiệm
Vậy có 6 điểm thỏa mãn yêu cầu đề bài
Lời giải:
$y'=3x^2-6mx+3(m^2-1)=0$
$\Leftrightarrow x^2-2mx+m^2-1=0$
$\Leftrightarrow x=m+1$ hoặc $x=m-1$
Với $x=m+1$ thì $y=-2m-2$. Ta có điểm cực trị $(m+1, -2m-2)$
Với $x=m-1$ thì $y=2-2m$. Ta có điểm cực trị $m-1, 2-2m$
$f''(m+1)=6>0$ nên $A(m+1, -2m-2)$ là điểm cực tiểu
$f''(m-1)=-6< 0$ nên $B(m-1,2-2m)$ là điểm cực đại
$BO=\sqrt{2}AO$
$\Leftrightarrow BO^2=2AO^2$
$\Leftrightarrow (m-1)^2+(2-2m)^2=2(m+1)^2+2(-2m-2)^2$
$\Leftrightarrow m=-3\pm 2\sqrt{2}$
Chọn C
Ta có y ' = 3 x 2 - 6 m x + 3 ( m 2 - 1 )
Hàm số (1) có cực trị thì PT y ' = 0 có 2 nghiệm phân biệt
⇔ x 2 - 2 m x + m 2 - 1 = 0 có 2 nhiệm phân biệt
Khi đó, điểm cực đại A ( m - 1 ; 2 - 2 m ) và điểm cực tiểu B ( m + 1 ; - 2 m )
Ta có O A = 2 O B ⇔ m 2 + 6 m + 1 = 0
