Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = ( 3 - x ) ( x 2 - 1 ) + 2 x , ∀ x ∈ R . Hỏi hàm số y = f ' ( x ) - x 2 - 1 có bao nhiêu điểm cực tiểu
A. 2
B. 3
C. 4
D. 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

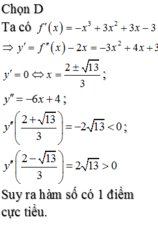

\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=3\end{matrix}\right.\) (chỉ quan tâm nghiệm bội lẻ)
\(g\left(x\right)=f\left(x^2-2x\right)\)
\(g'\left(x\right)=2\left(x-1\right)f'\left(x^2-2x\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\f'\left(x^2-2x\right)=0\end{matrix}\right.\)
\(f'\left(x^2-2x\right)=0\Rightarrow\left[{}\begin{matrix}x^2-2x=-2\\x^2-2x=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
BBT:
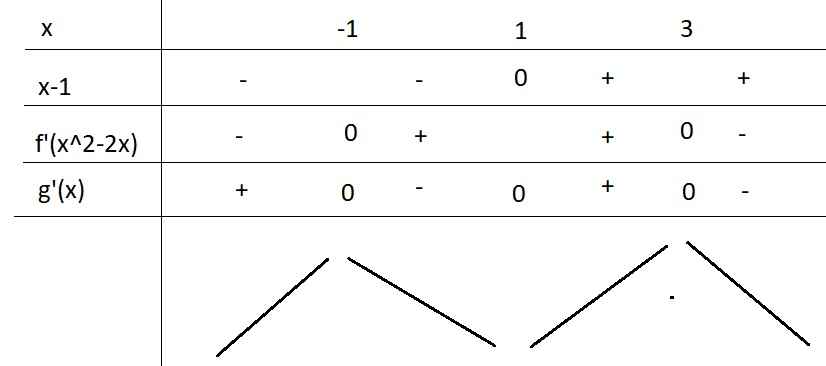
Từ BBT ta thấy \(f\left(x^2-2x\right)\) có 1 cực tiểu