Chọn ngẫu nhiên một số tự nhiên nhỏ hơn 300. Gọi A là biến cố “số được chọn không chia hết cho 3”. Tính xác suất P(A) của biến cố A.
A. P A = 2 3
B. P A = 124 300
C. P A = 1 3
D. P A = 99 300
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 6 2019
Chọn A
Có 300 số tự nhiên nhỏ hơn 300 nên n( Ω ) = 300.
Số các số tự nhiên nhỏ hơn 300 mà chia hết cho 3 là: (297-0):3 + 1 = 100.
Số các số tự nhiên nhỏ hơn 300 mà không chia hết cho 3 là: 300 - 100 = 200 nên n(A) = 200.
Vậy 
CM
27 tháng 7 2017
Chọn B
* Số các số tự nhiên nhỏ hơn 300 là 300 số. Lấy ngẫu nhiên một số tự nhiên nhỏ hơn 300 có suy ra n( Ω ) = 300
* Gọi A là biến cố “số được chọn không chia hết cho 4”, khi đó A ¯ là biến cố “số được chọn
chia hết cho 4”.
* Gọi số tự nhiên nhỏ hơn 300 và chia hết cho 4 là 4n (n ∈ ℕ )
* Ta có 
suy ra 
Do đó 
9 tháng 5 2023
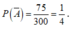
a: Biến cố ngẫu nhiên: A
Biến cố chẵc chắn: B
Biến cố ko thể: C
b: n(A)=3
=>P(A)=3/6=1/2
Số phần tử của không gian mẫu: n Ω = 300
Số các số tự nhiên nhỏ hơn 300 mà chia hết cho 3 là:
Chọn: A