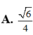
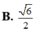
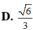
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Phương pháp: Sử dụng phương pháp xác định tâm mặt cầu ngoại tiếp khối chóp.
Cách giải: Đặt A(x;0;0), B(0;y;0), (x,y > 0)
Vì OA + OB = OC = 1 => x + y = 1
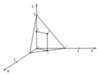
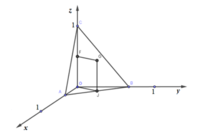
Gọi J, F lần lượt là trung điểm AB, OC. Kẻ đường thẳng qua F song song OJ, đường thẳng qua J song song OC, 2 đường thẳng này cắt nhau tại G.
∆OAB vuông tại O => J là tâm đường tròn ngoại tiếp tam giác.
GJ // OC => GJ ⊥ (OAB) => GO = GA = GB
GF // JO, JO ⊥ OC => GF ⊥ OC, mà F là trung điểm của OC
=>GF là đường trung trực của OC => GC = GO
=> GO = GA = GB = GC => G là tâm mặt cầu ngoại tiếp tứ diện OABC
Bán kính mặt cầu ngoại tiếp tứ diện OABC :
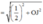
Ta có:
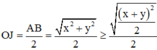
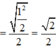
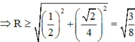
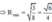
Đáp án C
Phương pháp: Sử dụng phương pháp xác định tâm mặt cầu ngoại tiếp khối chóp.
Cách giải: Đặt A(x;0;0), B(0;y;0), (x,y>0)
Vì OA+OB=OC = 1 => x+y=1
Gọi J, F lần lượt là trung điểm AB, OC. Kẻ đường thẳng qua F song song OJ, đường thẳng qua J song song OC, 2 đường thẳng này cắt nhau tại G
Tam giác OAB vuông tại O => J là tâm đường tròn ngoại tiếp tam giác
mà F là trung điểm của OC
=>GF là đường trung trực của OC => GC=GO
=> GO=GA=GB=GC=> G là tâm mặt cầu ngoại tiếp tứ diện OABC.
Bán kính mặt cầu ngoại tiếp tứ diện OABC
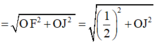
Ta có:
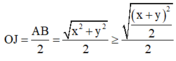
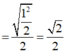
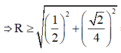
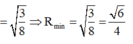
Giả sử
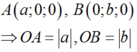
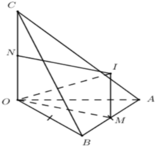
Tứ diện OABC có OA, OB, OC đôi một vuông góc.
Gọi M, N lần lượt là trung điểm của AB và OC.
Ta có
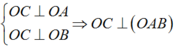
Qua M dựng đường thẳng song song với OC, qua N dựng đường thẳng song song với OM. Hai đường thẳng này cắt nhau tại I.
∆ O A B vuông tại O ⇒ M là tâm đường tròn ngoại tiếp ∆ O A B ⇒ I A = I B = I O .
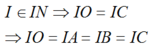
I là tâm mặt cầu ngoại tiếp O.ABC
Ta có
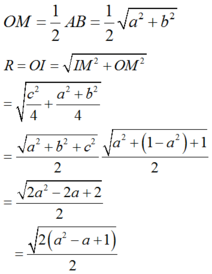
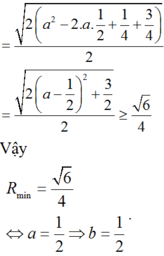
Chọn A.
Chọn D
Tứ diện OABC có ba cạnh đôi một vuông góc không phải là hình chóp đều.
Xét tam giác ODB và tam giác OAC có: OD = OA
góc AOC = góc BOD (=90o)
OB = OC
=> tam giác ODB = tam giác OAC (c.g.c)=> AC = BD (2 cạnh t,ư )
b/Ta có góc DOC + COB = zOx = 90o
AOB + BOC = tOy = 90o
=> góc DOC = AOB mà OD =OA, OC = OB
=> tam giác ODC = OAB (c.g.c) => DC = AB (1)
Dễ có tam giác DCB = ABC (Vì BC chung, DC=AB,DB =AC )
=> góc CDB = CAB (2 góc t.ư) (2)
Dễ có tam giác CDA = BAD (vì AD chung, CD = AB, DB =AC ) => góc DCA = góc DBA (2 góc t.ư) (3)
Từ (1)(2)(3) => tam giác IDC =IAB (g.c.g)
=> ID = IA, IC = IB (cặp canh tương ứng )
Dễ có tam giác OIC = OIB (c.c.c)
=> góc COI = góc BOI (2 góc t.ư)
=> tia OI là phân giác của góc xOy
Chọn A