Khi thiết kế vỏ lon sữa hình trụ các nhà thiết kế luôn đặt mục tiêu sao cho chi phí làm vỏ lon nhỏ nhất. Muốn thể tích khối trụ là V mà diện tích toàn phần của hình trụ nhỏ nhất thì bán kính R của đường tròn đáy khối trụ bằng?
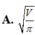
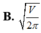
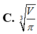
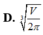
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có V t = V = l . π R 2 ⇒ l = V π R 2
S t = l .2 π R + 2 π R 2 ⇒ S t = V π R 2 π R + 2 π R 2 = 2 ( π R 2 + V R )
S t = 2 ( π R 2 + V 2 R + V 2 R ) ≥ 2.3 π R 2 . V 2 R . V 2 R 3 = 6 π V 2 4 3
Dấu “=” xảy ra khi và chỉ khi π R 2 = V 2 R ⇔ R = V 2 π 3

Chọn đáp án A.
Gọi r, h lần lượt là bán kính đáy và chiều cao của lon sữa bò cần thiết kế.

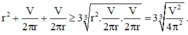
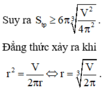

Đáp án: 28,1
Giải thích các bước giải:
a) Đường kính đáy của hình nón đó là:
d = 2 . r = 2 . 2 = 4
Vì chiều cao của hình nón đó bằng đường kính đáy của hình nón đó nên chiều cao h của hình nón đó là: h = 4 (cm)
Ta có: l² = r² + h² (theo định lý Py - ta - go)
⇒ l = √(r² + h²) = √(2² + 4²) = √(4 + 16) = √20 (cm)
Diện tích xung quanh của hình nón đó là: Sxq = π . r . l = π . 2 . √20 ≈ 28,1(cm²)
Vậy diện tích xung quanh của hình nón đó là ≈ 28,1
Chọn D