Cho I = ∫ 1 2 x + ln x x + 1 2 dx = a b ln 2 - 1 c với a, b, c là các số nguyên dương và các phân số là phân số tối giản.
Tính giá trị của biểu thức S = a + b c .
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(I=\int\limits^e_1\frac{\frac{1-lnx}{x^2}}{\left(1+\frac{lnx}{x}\right)^2}dx\)
Đặt \(\frac{lnx}{x}=t\Rightarrow\left(\frac{1-lnx}{x^2}\right)dx=dt\)
\(\Rightarrow I=\int\limits^{\frac{1}{e}}_0\frac{dt}{\left(1+t\right)^2}=-\frac{1}{1+t}|^{\frac{1}{e}}_0=\frac{1}{e+1}\)
\(\Rightarrow a=b=1\Rightarrow a^2+b^2=2\)

a/ Tích phân này làm sao giải được nhỉ?
b/ Đặt \(\sqrt{x}=t\Rightarrow x=t^2\Rightarrow dx=2t.dt\)
\(I=\int\frac{2t^2.dt}{4-t^4}=\int\left(\frac{1}{2-t^2}-\frac{1}{2+t^2}\right)dt=\frac{1}{2\sqrt{2}}ln\left|\frac{\sqrt{2}+t}{\sqrt{2}-t}\right|+\frac{1}{\sqrt{2}}arctan\frac{\sqrt{2}}{t}+C\)
\(=\frac{1}{2\sqrt{2}}ln\left|\frac{\sqrt{2}+\sqrt{x}}{\sqrt{2}-\sqrt{x}}\right|+\frac{1}{\sqrt{2}}arctan\frac{\sqrt{2}}{\sqrt{x}}+C\)
c/ \(I=\int\frac{\sqrt{1+x^2}}{x^2}.xdx\)
Đặt \(\sqrt{1+x^2}=t\Rightarrow x^2=t^2-1\Rightarrow xdx=tdt\)
\(\Rightarrow I=\int\frac{t^2dt}{t^2-1}=\int\left(1+\frac{1}{t^2-1}\right)dt=t+ln\left|\frac{t-1}{t+1}\right|+C=\sqrt{1+x^2}+ln\left|\frac{\sqrt{1+x^2}-1}{\sqrt{1+x^2}+1}\right|+C\)
d/ Con nguyên hàm này cũng không tính được, chắc bạn ghi nhầm đề
Chọn A
Ta có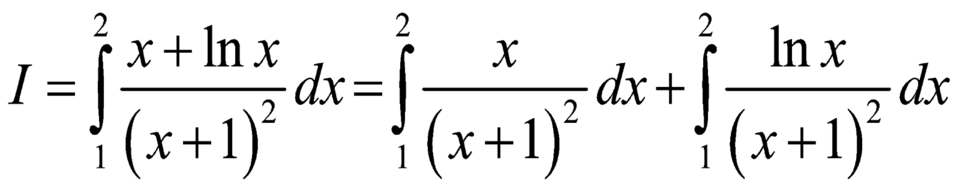 .
.
Xét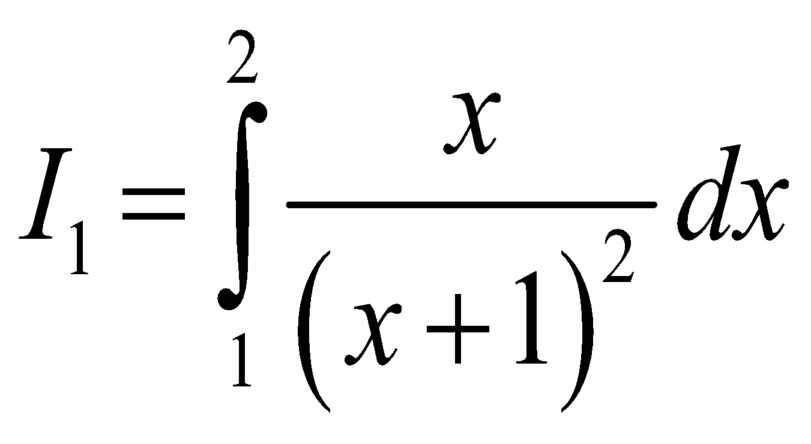 .
.
Đặt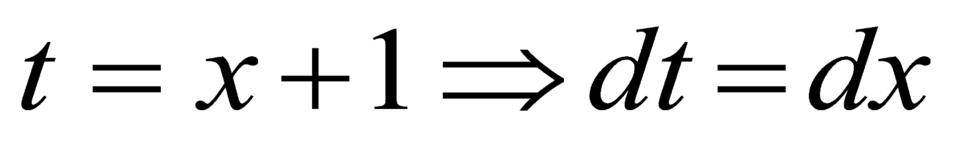 .
.
Do đó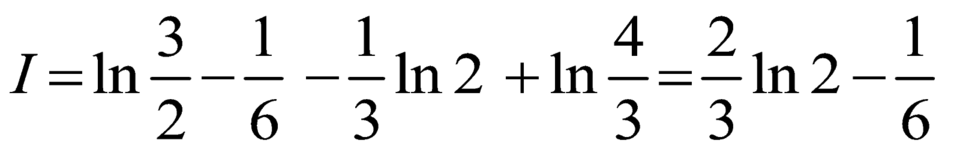 .
.