Bên cạnh con đường trước khi vào thành phố người ta xây một ngọn tháp đèn lộng lẫy. Ngọn tháp hình tứ giác đều S.ABCD cạnh bên
S
A
=
600
mét,
A
S
B
=
15
°
. Do sự cố đường dây điện tại điểm Q (là trung điểm của SA) bị hỏng, người ta tạo ra một con đường từ A đến Q gồm bốn đoạn thẳng: AM, MN, NP, PQ (hình vẽ). Để tiết kiệm kinh phí, kỹ sư đã...
Đọc tiếp
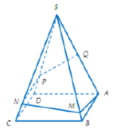
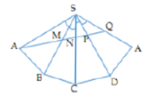
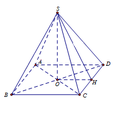
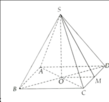
Bên cạnh con đường trước khi vào thành phố người ta xây một ngọn tháp đèn lộng lẫy. Ngọn tháp hình tứ giác đều S.ABCD cạnh bên S A = 600 mét, A S B = 15 ° . Do sự cố đường dây điện tại điểm Q (là trung điểm của SA) bị hỏng, người ta tạo ra một con đường từ A đến Q gồm bốn đoạn thẳng: AM, MN, NP, PQ (hình vẽ). Để tiết kiệm kinh phí, kỹ sư đã nghiên cứu và nó được chiều dài con đường từ A đến Q ngắn nhất.
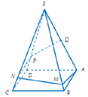
Tính tỷ số k = A M + M N N P + P Q
A. k = 2
B. k = 4 3
C. k = 3 2
D. k = 5 3
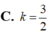
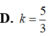
Đáp án A
Phương pháp:
Trải 4 mặt của hình chóp ra mặt phẳng và tìm điều kiện để A M + M N + N P + P Q là nhỏ nhất.
Cách giải:
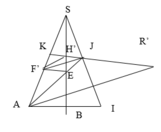
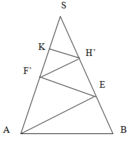
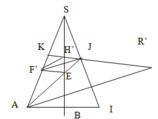
Ta “xếp” 4 mặt của hình chóp lên một mặt phẳng, được như hình bên:
Như hình vẽ ta tháy, để tiết kiệm dây nhất thì các đoạn AM, MN, NP, PQ phải tạo thành một đoạn thẳng AQ.
Lúc này, xét Δ S A Q có:
A S M = M S N = N S P = P S Q = 15 °
S A = 600 m , S Q = 300 m
⇒ k = A M + M N N P + P Q = A N N Q = S A S Q = 2
(Vì A N N Q = S A S Q do tính chất của đường phân giác SN).