Cho hình chóp SABC , ΔABC vuông cân tại A , SA ⊥ ABC , BC = a , SBC , ABC = 45 o . Trên tia đối của tia SA lấy điểm R sao cho RS=2SA . Tính VRABC.
A. a 3 12
B. a 3 8
C. a 3 24
D. a 3 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


![]()
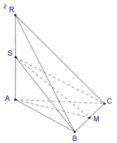

Đáp án A
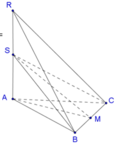
Gọi M là trung điểm của BC. Dễ thấy S M A ^ = 45 °
Tam giác ABC vuông cân tại A suy ra ![]()
Tam giác SAM vuông tại A, S M A ^ = 45 ° suy ra SA = AM = a 2
Vậy 
Mà

Đáp án B

Gọi M là trung điểm của BC . Vì Δ A B C cân tại A nên A M ⊥ B C ,
Ta có A M ⊥ B C S M ⊥ B C S B C ∩ A B C = B C
->Góc giữa S B C và A B C là góc S M A Vì góc S A M = 90 0
Có B M = a , góc B A M = 60 0 nên
sin B A M = B M A B ⇒ A B = 2 a 3 ⇒ S Δ A B C = 1 2 A B . A C . sin 120 0 = a 2 3 3
tan B A M = B M A M ⇒ A M = a 3 ⇒ tan S M A = S A A M ⇒ S A = a 3
V S . A B C D = 1 3 . a 3 . a 2 3 3 = a 3 9

\(SB=\sqrt{\left(a\sqrt{3}\right)^2+a^2}=2a\)
\(SC=\sqrt{SA^2+AC^2}=a\sqrt{5}\)
Vì SB^2+BC^2=SC^2
nên ΔSBC vuông tại B
(SBC;ABC)=(SB;BA)=góc SBA=60 độ

Đáp án B
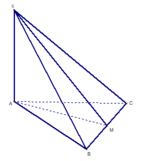
Gọi M là trung điểm của BC . Vì Δ A B C cân tại A nên A M ⊥ B C ,
Ta có A M ⊥ B C S M ⊥ B C S B C ∩ A B C = B C ⇒ Góc giữa S B C và A B C là góc Vì góc S A M = 90 0
Có B M = a , góc B A M = 60 0 nên
sin B A M = B M A B ⇒ A B = 2 a 3 ⇒ S Δ A B C = 1 2 A B . A C . sin 120 0 = a 2 3 3
tan B A M = B M A M ⇒ A M = a 3 ⇒ tan S M A = S A A M ⇒ S A = a 3
V S . A B C D = 1 3 . a 3 . a 2 3 3 = a 3 9

\(AB=AC=\dfrac{BC}{\sqrt{2}}=\dfrac{3a}{\sqrt{2}}\)
\(\Rightarrow V_{SABC}=\dfrac{1}{3}SA.\dfrac{1}{2}AB.AC=\dfrac{1}{3}.2a.\dfrac{1}{2}.\left(\dfrac{3a}{\sqrt{2}}\right)^2=\dfrac{3a^3}{2}\)