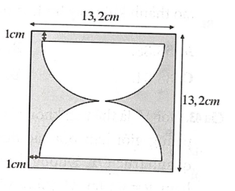
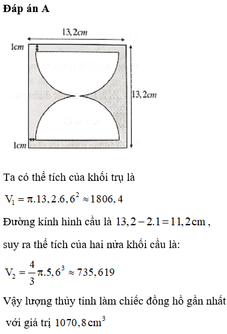
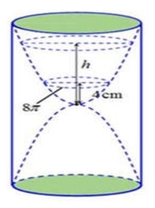
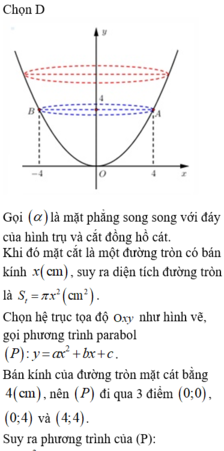
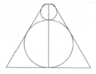
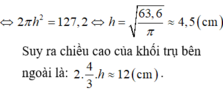Một xưởng sản xuất muốn tạo ra những chiếc đồng hồ cát thủy tinh có dạng hình trụ, phần chứa cát là hai nửa hình cầu bằng nhau. Hình vẽ bên với kích thước đã cho là bản thiết kế thiết diện qua trục của chiếc đồng hồ này (phần giới hạn bởi hình trụ và phần hai nữa hình cầu chứa cát). Khi đó, lượng thủy tinh làm chiếc đồng hồ cát gần nhất với giá trị nào trong các giá trị sau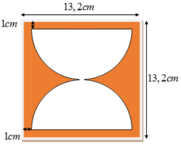
![]()
![]()
![]()
![]()