Cho hình thoi ABCD biết độ dài hai đường chéo lần lượt là 6 cm và 8 cm giao điểm của hai đường chéo là H. a Tính độ dài đoạn AB. b. Tính khoảng cách từ điểm H đến AB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 10 2021
Vì ABCD là hình thoi nên \(AB=BC=CD=DA=20\left(cm\right)\)
Và AC cắt BD tại O nên O là trung điểm AC,BD
\(\Rightarrow AC=2AO=32\left(cm\right);BD=2OB=24\left(cm\right)\)
16 tháng 12 2021
OB = 12 cm => BD = 2.12 = 24 cm
OA = 16 cm => AC = 2.16 = 32 cm
AB = BC = CD = AD = 20 cm (hình thoi có 4 cạnh bằng nhau)
TM
2
27 tháng 4 2017
1/ S hình thoi :
18 x 33 : 2 = 297 ( dm2 )
ĐS : 297 dm2
2/ Độ dài đường chéo còn lại : 4/3 : 8/5 x 2 = 5/3 ( cm2 )
ĐS : 5/3 cm2
3/ Độ dài đường chéo thứ 2 : 42 x 2/3 = 28 ( cm )
S : 42 x 28 : 2 = 588 ( cm2 )
ĐS : 28 cm2
4/ Tổng độ dài 2 đường chéo : 41 x 2 = 82 ( cm )
Độ dài đường chéo lớn : ( 82 + 28 ) : 2 = 55 ( cm )
Độ dài đường chéo bé : 55 - 28 = 27 ( cm )
S : 55 x 27 : 2 = 742, 5 ( cm2 )
ĐS : 742,5 cm2
5 tháng 6 2017
Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
9 tháng 7 2019
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath
CM
1 tháng 8 2019
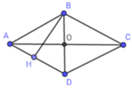
Giả sử hình thoi ABCD, đường chéo AC vuông góc với BD tại O, AC = 8 cm; BD = 6 cm.
Gọi BH là đường cao hình thoi kẻ từ đỉnh B.
Ta có: DO = 1 2 BD = 1 2 .6 = 3 (cm);
AO = 1 2 AC = 1 2 .8 = 4 (cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOD vuông tại O ta có:
AD = A O 2 + O D 2 = 4 2 + 3 2 = 5 (cm)
SABCD = 1 2 BD. AC = 1 2 6.8 = 24 (cm2)
SABCD = BH. AD => BH = S A B C D A D = 24 5 = 4, 8 (cm)
Đáp án cần chọn là: B
Giúp với