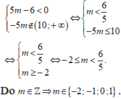Có bao nhiêu giá trị m nguyên để hàm số y = 2 x 2 + m x + 2 3 2 xác định với mọi x ∈ R ?
A. 5
B. 4
C. 7
D. 9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
11 tháng 4 2019
Đúng(0)
Những câu hỏi liên quan
CM
23 tháng 12 2017
Chọn C
Hàm số f(x) =
2
x
2
+
m
x
+
2
3
2
xác định với mọi
x
∈
ℝ
Vì m nguyên nên 
Vậy có tất cả 7 giá trị m thỏa mãn điều kiện đề bài.
20 tháng 5 2022
2:
a: Thay x=1 vào (P), ta được:
\(y=\dfrac{1^2}{2}=\dfrac{1}{2}\)
Thay x=1 và y=1/2 vào (D), ta được:
\(m-1=\dfrac{1}{2}\)
hay m=3/2
b: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2+x-m=0\)
\(\text{Δ}=1^2-4\cdot\dfrac{1}{2}\cdot\left(-m\right)=2m+1\)
Để (D) cắt (P) tại hai điểm phân biệt thì 2m+1>0
hay m>-1/2
c: Để (D) tiếp xúc với (P) thì 2m+1=0
hay m=-1/2
CM
14 tháng 11 2019
+ Xét hàm số f( x) = x3- x2+ ( m2+ 1) x- 4m- 7 trên đoạn [ 0; 2]
Ta có f’ (x) = 3x2- 2x+ m2+ 1= 3( x-1/3) 2+ m2+ 2/3> 0 .
+ Suy ra hàm số f(x) đồng biến trên
0 ; 2 ⇒ m i n [ 0 ; 2 ] f ( x ) = f ( 0 ) = - 4 m - 7 m a x [ 0 ; 2 ] f ( x ) = f ( 2 ) = 2 m 2 - 4 m - 1
+ Khi đó
m a x [ 0 ; 2 ] y = m a x [ 0 ; 2 ] f ( x ) = m a x - 4 m - 7 ; 2 m 2 - 4 m - 1 ≤ 15 ⇔ - 4 m - 7 ≤ 15 2 m 2 - 4 m - 1 ≤ 15 ⇔ - 11 2 ≤ m ≤ 2 2 m 2 - 4 m - 16 ≤ 0 ⇔ - 11 2 ≤ m ≤ 2 - 2 ≤ m ≤ 4 ⇔ - 2 ≤ m ≤ 2 → m ∈ ℤ m ∈ ± 2 ; ± 1 ; 0
Vậy có 5 giá trị thoả mãn.
Chọn C.
CM
24 tháng 9 2017
Đáp án C
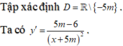
Để hàm số nghịch biến trên khoảng ( 10 ; + ∞ ) thì
