Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
B là khẳng định sai
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
\(CD=\left(SCD\right)\cap\left(BCD\right)\)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SDC) và (BCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{2}\Rightarrow\widehat{SDA}\approx54^044'\)
Chọn C
Để cho gọn ta chọn a=2
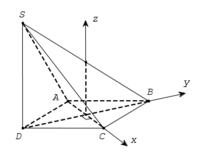
Chọn hệ trục tọa độ Oxyz như hình vẽ với O(0;0;0) và C(1;0;0), B(0; 3 ;0) S(0; - 3 ; x) với x =SD>0
Suy ra A(-1;0;0) và D(0;- 3 ;0)
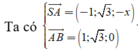
VTPT của mặt phẳng (SAB) là
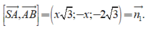
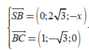
VTPT của mặt phẳng (SBC) là
Từ giả thiết bài toán, ta có
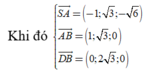
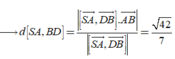
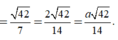
a: Qua S kẻ đường Sx song song SD
=>Sx vuông góc SA
SC vuông góc CD
=>SC vuông góc Sx
((SAB);(SCD))=góc ASC
b: (SBD) căt (SAB)=SB
Kẻ DA vuông góc AB
mà DA vuông góc SA
nên DA vuông góc (SAB)
=>DA vuông góc SB
Kẻ AK vuông góc SB
=>((SBD);(SAB))=góc AKD
c: (SBC) giao (SCD)=SC
Kẻ BH vuông góc SC
Qua H kẻ HF//CD
=>HF vuông góc SC
=>((SBC);(SCD))=góc BHF
Đáp án là A
Từ giả thiết , ta có SA ⊥ (ABC): B đúng
Ta có :
=> C đúng.
Ta có:
=> D đúng.
Do đó : A sai . Chọn A.
Nhận xét : Ta có cũng có thể giải như sau:
Mà (SCD) và (SAD) không song song hay
Trùng nhau nên CD ⊥ (SCD) là sai . Chọn A.