Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\left(m^2-3m-5\right)x-y-2m+19=0\)
\(\Leftrightarrow y=\left(m^2-3m-5\right)x-2m+19\)
Ta có:
\(f'\left(x\right)=-3x^2+4x-1\)
\(f'\left(2\right)=-5\)
Phương trình tiếp tuyến tại A:
\(y=-5\left(x-2\right)+3\Leftrightarrow y=-5x+13\)
Để hai đường thẳng song song:
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-3m-5=-5\\-2m+19\ne13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-3m=0\\2m\ne6\end{matrix}\right.\)
\(\Leftrightarrow m=0\)
a. Đồ thì hàm số song song với y=3x là y=3x + b
Cho x = 0 thì y = b, ta được điểm A(0;b) thuộc trục tung Oy
Cho y = 0 thì x = -\(\frac{\text{b}}{a}\), ta được B(-\(\frac{\text{b}}{a}\);0) thuộc trục hoành Ox
Theo đề bài, ta có đồ thị hàm số căt trục hoành tại điểm có hoành độ bằng -3
Vậy : \(-\frac{b}{a}\) = -3 hay \(-\frac{b}{3}\) = -3 => b = 9
Ta có 2 điểm : A(0;9) thuộc trục tung Oy
B(-3;0) thuộc trục hoành Ox
Câu 1:
\(f'\left(1\right)=g'\left(1\right)=k\)
\(h\left(x\right)=\frac{f\left(x\right)+2}{g\left(x\right)+1}\Rightarrow h'\left(x\right)=\frac{f'\left(x\right)\left[g\left(x\right)+1\right]-g'\left(x\right)\left[f\left(x\right)+2\right]}{\left[g\left(x\right)+1\right]^2}\)
\(\Rightarrow h'\left(1\right)=\frac{k\left(b+1\right)-k\left(a+2\right)}{\left(b+1\right)^2}=\frac{k\left(b-a-1\right)}{\left(b+1\right)^2}\)
Mà \(h'\left(1\right)=k\Rightarrow k=\frac{k\left(b-a-1\right)}{\left(b+1\right)^2}\Rightarrow\frac{b-a-1}{\left(b+1\right)^2}=1\)
\(\Leftrightarrow b-a-1=\left(b+1\right)^2\Rightarrow a=b-1-\left(b+1\right)^2\)
\(\Rightarrow a=-b^2-b-2\)
Câu 2:
\(y=f\left(x\right)=\frac{x+1}{x-2}\Rightarrow f'\left(x\right)=\frac{-3}{\left(x-2\right)^2}\)
Phương trình hoành độ giao điểm:
\(\frac{x+1}{x-2}=x+m\Leftrightarrow x+1=\left(x+m\right)\left(x-2\right)\)
\(\Leftrightarrow x^2+\left(m-3\right)x-2m-1=0\)
\(\Delta=\left(m-3\right)^2+4\left(2m+1\right)=\left(m+1\right)^2+12>0\)
\(\Rightarrow\) d luôn cắt (P) tại 2 điểm phân biệt A và B có hoành độ giả sử là a và b
Theo Viet: \(\left\{{}\begin{matrix}a+b=3-m\\ab=-3m-1\end{matrix}\right.\) \(\Rightarrow3a+3b-ab=10\) (1)
Mặt khác do tiếp tuyến tại A và B song song
\(\Leftrightarrow\frac{-3}{\left(a-2\right)^2}=\frac{-3}{\left(b-2\right)^2}\Leftrightarrow\left[{}\begin{matrix}a-2=b-2\\a-2=2-b\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}a=b\\a=4-b\end{matrix}\right.\)
TH1: \(a=b\) thay vào (1):
\(\Rightarrow-a^2+6a-10=0\left(vn\right)\)
TH2: \(a=4-b\)
\(\Rightarrow a+b=4\Rightarrow3-m=4\Rightarrow m=-1\)
Pt hoành độ giao điểm của đồ thị hàm số (C) với đường thẳng d là:
\(\dfrac{x-1}{x+1}=m-x\Leftrightarrow\left\{{}\begin{matrix}x\ne-1\\g\left(x\right)=x^2+\left(2-m\right)x-m-1=0\left(1\right)\end{matrix}\right.\)
Đồ thị (C) cắt đường thẳng d tại 2 điểm phân biệt <=> pt(1) có 2 nghiệm phân biệt khác -1
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\g\left(-1\right)\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2+8>0\\-2\ne0\end{matrix}\right.\)
Khi đó: \(x_A,x_B\) là nghiệm của pt (1). Vì tiếp tuyến tại A và B //
\(\Rightarrow f'\left(x_A\right)=f'\left(x_B\right)\Leftrightarrow\dfrac{2}{\left(x_A+1\right)^2}=\dfrac{2}{\left(x_B+1\right)^2}\Leftrightarrow\left[{}\begin{matrix}x_A=x_B\left(loai\right)\\x_A+x_B=-2\end{matrix}\right.\)
Theo định lí Viet ta có:
\(x_A+x_B=m-2\Rightarrow m-2=-2\Leftrightarrow m=0\)
TXĐ: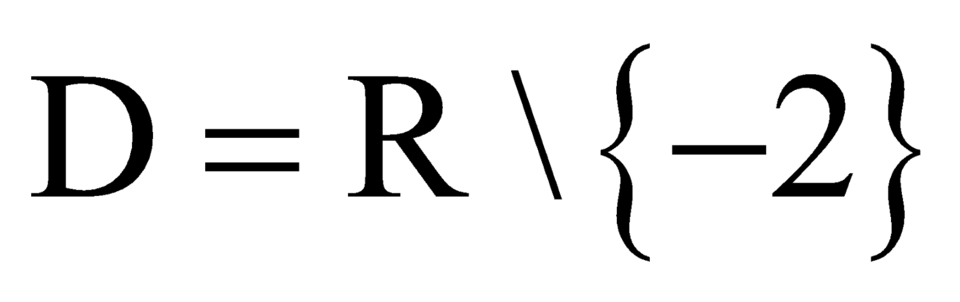
.
Ta có: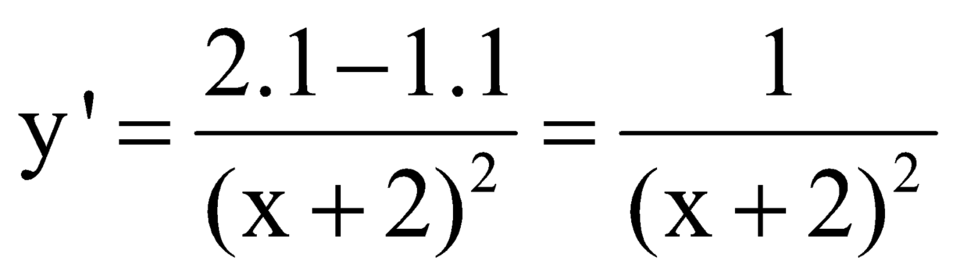
Gọi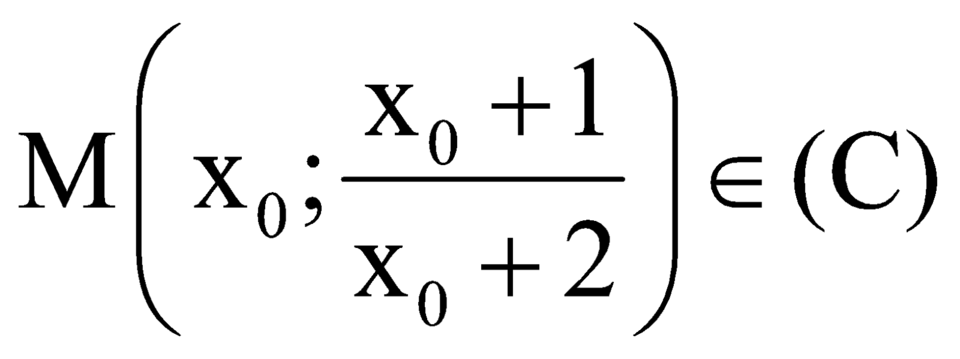
Ta có phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ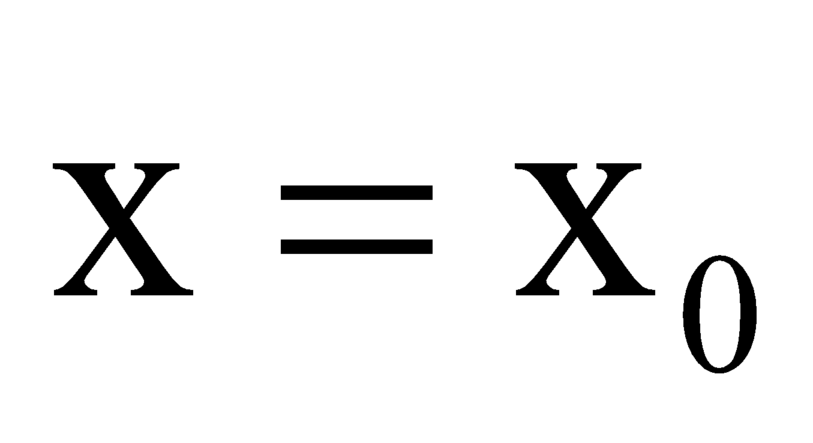
là:
Để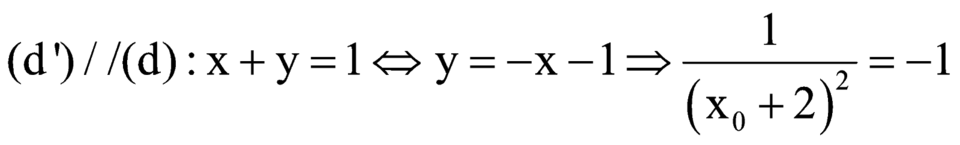
(vô nghiệm)
Chọn A.
Chú ý: Phải đưa phương trình đường thẳng (d) về dạng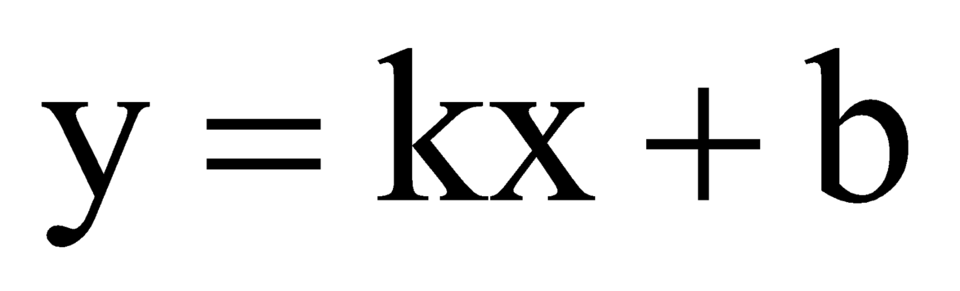
và xác định hệ số góc của đường thẳng d cho chính xác, tránh sai lầm khi cho hệ số góc của đường thẳng d trong bài toán này bằng 1