ho góc vuông xOy, điểm A thuộc tia Ox, điểm B thuộc tia Oy. Đường trung trực của đoạn thẳng OA cắt Ox ở D, đường trung trực của đoạn thẳng OB cắt Oy ở E. Gọi C là giao điểm của hai đường trung trực đó. Chứng minh rằng:
Ba điểm A, B, C thẳng hàng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 2 2019
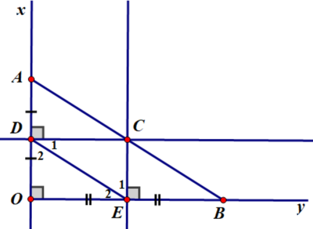
Hai tam giác vuông ΔDCE và ΔCDA có :
CD chung
CE = AD (do ∆BCE = ∆CDA)
⇒ ∆DCE = ∆CDA (hai cạnh góc vuông)
26 tháng 4 2015
bài toán này khó wa.mí bn help mk vs.kẻ hình hộ thì càng tốt nun.thanks nhiều nha!!!!!!^^^
17 tháng 11 2017
tu lam di roi viet len cac cau ko bt thi tu di ma hoi nhau
hay cho to 1 diem la dung
giup minh nhe !
TP
Thảo Phương
CTVVIP
19 tháng 4 2017
c) Chứng minh CA = CB
- Vì C nằm trên đường trung trực của OA nên CA = CO (3)
- Vì C nằm trên đường trung trực của OB nên CB = CO (4)
Từ (3) và (4) suy ra: CA = CB (đpcm).
19 tháng 4 2017
c) Chứng minh CA = CB
- Vì C nằm trên đường trung trực của OA nên CA = CO (3)
- Vì C nằm trên đường trung trực của OB nên CB = CO (4)
Từ (3) và (4) suy ra: CA = CB (đpcm).
Chứng minh tương tự như d suy ra CB // DE.
Do đó theo tiên đề Ơ-clit ta suy ra hai đường thẳng BC và CA trùng nhau hay A, B, C thẳng hàng.