Tính thể tích V của khối lập phương ABCD.A'B'C'D' biết đường chéo AC'=a 3 .
A. a 3 3
B. 3 3 a 3
C. 3 6 a 3 4
D. a 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Giả sử cạnh của hình lập phương là a. Khi đó AB' = x
2
. Xét tam giác vuông AB’C’ vuông tại B’ ta có ![]()
![]() .
.
Do đó ![]()
![]()

Đáp án A
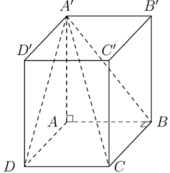
Ta có: hình lập phương ABCD.A'B'C'D' có đường chéo bằng a 3
Suy ra cạnh của hình lập phương bằng a.
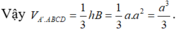 Vậy
V
A
'
.
A
B
C
D
=
1
3
h
B
=
1
3
a
.
a
2
=
a
3
3
Vậy
V
A
'
.
A
B
C
D
=
1
3
h
B
=
1
3
a
.
a
2
=
a
3
3

\(AC=AB\sqrt{2}=4a\)
Áp dụng định lý Pitago:
\(CC'=\sqrt{\left(AC'\right)^2-AC^2}=3a\)
\(\Rightarrow V=3a.\left(2a\sqrt{2}\right)^2=24a^3\)
Chọn D.
Gọi cạnh hình lập phương là x. Ta có