Tìm tất cả các giá trị thực của tham số m để hàm số y = m sin x + 1 3 sin 3 x đạt cực đại tại điểm x = π 3 .
A. m = 0
B. m = 1
C. m = − 2
D. m = 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Ta có: y’ = cos 3x + mcos x
Hàm số đạt cực đại tại
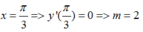
m = 2 => y’ = cos 3x + 2cos x => y’’ = -3sin 3x – 2sin x
=>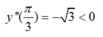
Vậy, m = 2

Đáp án C
Ta có: y ' = cos 3 x + m . cos x và y ' ' = − 3 sin 3 x − m . sin x
Để hàm số đạt cực đại tại:
x = π 3 ⇒ y ' π 3 = 0 ⇒ − 1 + m 2 = 0 ⇔ m = 2.
Với m = 2 ⇒ y ' ' π 3 = − 3 sin π − 2 sin π 3 < 0
nên hàm số đạt cực đại tại x = π 3

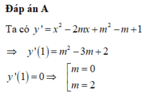
+ Với m=0 khi đó phương trình y’ = 0 sẽ có nghiệm kép nên loại.
+ Với m=2 thì khi đó phương trình y’=0 có hai nghiệm.
Chọn phương án A.

Đáp án B
Ta có y ' = x 2 − m 2 + 1 x + 3 m − 2 , y ' ' = 2 x − m 2 − 1
Hàm số đạt cực đại tại x = 1 ⇒ y ' 1 = 0 ⇔ 1 − m 2 + 1 + 3 m − 2 = 0 ⇔ m = 1 m = 2
Với m = 1 ⇒ y ' ' = 2 x − 2 ⇒ y ' ' 1 = 0
Với m = 2 ⇒ y ' ' = 2 x − 5 ⇒ y ' ' 1 = − 3
Suy ra hàm số đạt cực tiểu tại x = 1 khi m = 2
Đáp án D
Ta có: y ' = m cos x + c os 3 x , y ' ' = m sin x − 3 sin 3 x .
Hàm số đạt cực đại tại x = π 3
⇒ y ' π 3 = 0 ⇔ m c os π 3 + c os 3 π 3 = 0 ⇒ m = 2.
Với m = 2 ⇒ y ' ' = − 2 sin x − 3 sin 3 x ⇒ y ' ' π 3 = − 3 .
Suy ra hàm số đạt cực đại tại điểm x = π 3 khi m=2.