Một xưởng in có 8 máy in, mỗi máy in được 3600 bản in trong một giờ. Chi phí để vận hành một máy trong mỗi lần in là 50 nghìn đồng. Chi phí cho n máy chạy trong một giờ là
10
6
n
+
10
nghìn đồng. Hỏi nếu in 50000 tờ quảng cáo thì phải sử dụng bao nhiêu máy để được lãi nhiều nhất? A. 4 máy. B. 6 máy. C. 5 máy. D. 7...
Đọc tiếp
Một xưởng in có 8 máy in, mỗi máy in được 3600 bản in trong một giờ. Chi phí để vận hành một máy trong mỗi lần in là 50 nghìn đồng. Chi phí cho n máy chạy trong một giờ là 10 6 n + 10 nghìn đồng. Hỏi nếu in 50000 tờ quảng cáo thì phải sử dụng bao nhiêu máy để được lãi nhiều nhất?
A. 4 máy.
B. 6 máy.
C. 5 máy.
D. 7 máy.
là số máy in sử dụng trong một giờ để được lãi nhiều nhất. Khi đó chi phí dành cho x máy in trong một giờ là nghìn đồng.
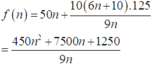
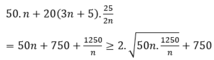
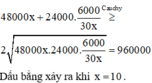
Đáp án C
Gọi f n là hàm chi phí in 50000 tờ quảng cáo 0 < n ≤ 8 ; n ∈ ℕ . Ta cần tìm n để f(n) có giá trị thấp nhất. Theo giả thiết f(n) bao gồm chi phí vận hành cho n máy là 50n nghìn đồng. Và chi phí chạy máy sản xuất 50000 tờ quảng cáo là: 50000 3600 n 10 6 n + 10 = 2500 9 n 3 n + 5
Vậy f ( n ) = 50 n + 2500 9 n 3 n + 5 = 50 n + 250 9 n + 2500 3
Đến đây ta có thể khảo sát hàm f(n) với nnguyên để tìm chi phí thấp nhất hoặc kiểm tra trực tiếp bốn đáp án và được kết quả thấp nhất với n=5.